Читайте также:
|
typedef struct vertex_typ
{
float x,y;
} vertex, *vertex_ptr;
// структура объекта
typedef struct object_typ
{
int num_vertices; // количество вершин в объекте
int color; // цвет объекта
float хо,уо; // позиция объекта
float x_velocity; // используем позже для
float y_velocity; // перемещения объекта
float scale; // коэффициент масштабирования
float angle; // угол поворота
vertex vertices[16]; // массив для определения 16 вершин
} object, *object_ptr;
Эта структура данных нам нужна для описания объекта, представляющего собой многоугольник определенного цвета и расположенного в определенной позиции на экране.
Позиционирование объекта
Теперь поговорим о строчке, которая определяет позицию объекта в структуре из Листинге 4.4. Координаты (хо,уо) описывают начальную позицию объекта на плоскости.
Многоугольник или объект рисуется относительно начальной позиции. Все это подводит нас к понятию относительной системы координат. Возможно, вы не знаете, что картезианская система называется еще мировой системой координат. Подразумевается, что она просто огромна. В то же самое время экран ПК имеет свою систему координат, называемую экранной. При этом все объекты на экране имеют свою, локальную систему координат. Это показано на рисунке 4.5.
Мы можем определить объект в локальной системе координат, затем преобразовать эти координаты в мировые и, наконец, нарисовать наш объект в экранной систем координат. Выглядит это достаточно долгим занятием, но на
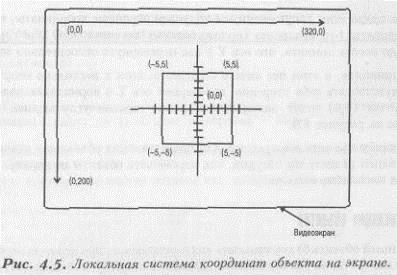
деле все оказывается несколько проще. Давайте договоримся, что у нас на компьютере мировые и экранные системы координат совпадают. Это значит, что:
§ Точка (0,0) находится в левом верхнем углу экрана;
§ При движении вправо увеличивается значение Х-координаты;
§ При перемещении вниз увеличивается Y-координата.
Благодаря этим допущениям мы получаем экранные координаты, похожие на координаты 1-го квадранта (положительные значения осей Х и Y), но при этом надо всегда помнить, что ось Y у нас перевернута относительно экрана.
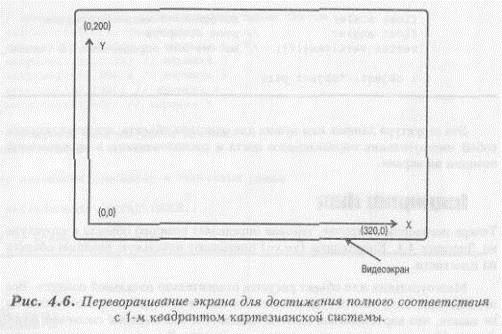
В принципе, в этом нет ничего страшного, хотя и несколько непривычно. Чтобы чувствовать себя уверенно, перевернем ось Y в нормальное положение. Тогда точка (0,0) будет находиться в левом нижнем углу экрана, как это показано на рисунке 4.6.
Теперь у нас есть все средства для представления объектов в компьютере. В следующем разделе мы обсудим, как перемещать объекты по экрану, поворачивать и масштабировать их.
Трансляция объектов
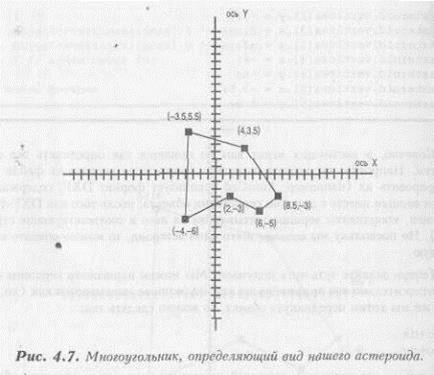Трансляцией объекта будем называть его перемещение, при котором не меняется ни угол поворота, ни размер объекта. Давайте воспользуемся нашей структурой данных для определения конкретного объекта, с которым будем экспериментировать и в дальнейшем. К примеру, пусть это будет астероид. На рисунке 4.7 показан его внешний вид. Листинг 4.5 содержит фрагмент, описывающий наш астероид.
Дата добавления: 2015-07-12; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Листинг 4.2. Программа, рисующая линии (LINER.С). | | | Листинг 4.5. Описание астероида. |