Способ. 3 страница

При изучении показателей рядов динамики (абсолютного прироста, темпов роста и прироста, абсолютного значения одного процента прироста и средних уровней) необходимо тщательно разобраться в способах их расчета, и взаимосвязях различных показателей. Расчет большей части этих показателей основан на сравнении между собой уровней ряда динамики. В результате образуются цепные и базисные показатели.

Абсолютный прирост (Δ y) определяется по формулам:

Δ y=y_i–y_{i -1} – цепной (10.1)

Δ y_i=y_i–y₀ – базисный (10.2)

где y_i – уровень i-ого периода;

y_{i -1} – уровень предшествующего периода;

y ₀ – уровень базисного периода.

Темп роста (Т_р) определяется по формуле:

- цепной (10.3)

- базисный (10.4)

Темп прироста (Т_пр) определяется по формуле:

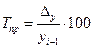- цепной (10.5)

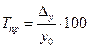- базисный (10.6)

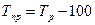(10.7)

Показатель абсолютного значения одного процента прироста (Δ_%) определяется по формулам:

(10.8)

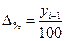(10.9)

Пример 10.1. Рассчитать основные показатели ряда динамики объема реализации продукции по предприятию.

Годы	Реализо-вано продук- ции, млн. грн.	Абсолютные приросты, млн. грн.	Темпы роста, %	Темпы прироста, %	Абсолют-ное значение 1% прироста, млн. грн.
к пред. году	к базис	к пред. году	к базис	к пред. году	к базис.
Т1	27,3	-	-			-	-	-
Т2	65,3	38,0	38,0	239,2	239,2	139,2	139,2	0,27
Т3	116,0	50,7	88,7	177,6	424,9	77,6	324,9	0,65
Т4	148,0	32,0	120,7	127,5	542,1	27,5	442,1	1,16
Т5	155,0	7.0	127,7	104,7	567,7	4,7	467,7	1,48
Т6	151,0	- 4,0	123,7	97,4	553,1	- 2,6	453,1	1,55

Методы расчёта среднего уровня ряда динамики зависят от его видов и способов получения статистических данных.

В интервальном ряду средний абсолютный уровень ряда (y) может быть определён по формуле средней арифметической простой (в рядах с равно стоящими уровнями) или взвешенной (в рядах с не равностоящими уровнями).

Среднее значение моментного ряда с равностоящими уровнями определяется по формуле средней хронологической:

(10.10)

В моментном ряду с неравными промежутками между датами:

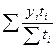= (10.11)

где n – число уровней ряда;

t – продолжительность периода.

Среднегодовой темп роста определяется по формулам:

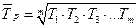(10.12)

(10.13)

Пример 10.2. Среднегодовой темп роста реализации продукции по данным примера 10.1 составит:

или 100,9 %

Средний темп прироста (Т_пр) определяется по формуле:

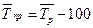(10.14)

Среднегодовой абсолютный прирост может быть вычислен двумя способами:

- как средняя арифметическая годовых приростов

(10.15)

- делением базисного прироста на число периодов

(10.16)

Следует обратить внимание на взаимосвязь показателей динамика, широко применяемых в расчётах:

- сумма последовательных цепных абсолютных приростов равна соответствующему базисному приросту;

- произведение последовательных цепных темпов роста равно базисному темпу за весь соответствующий период.

Вопросы и тесты для самоконтроля

10.1. Какие задачи статистического анализа решаются на основе динамических рядов?

10.2. Особенности интервальных и моментных рядов динамики.

10.3. Как рассчитываются средние уровни в моментном ряду динамики?

10.4. Экономический смысл абсолютных приростов и темпов роста.

10.5. Как изменяются темпы роста при стабильных абсолютных приростах?

10.6. Какова взаимосвязь между цепными и базисными показателями динамики?

10.7. Экономический смысл темпа прироста. Почему с темпами прироста не производятся арифметические действия?

10.8. От чего зависит абсолютное значение 1% прироста?

10.9. Какую задачу анализа решает коэффициент опережения?

10.10. Взаимосвязь темпов роста с относительными величинами планового задания и выполнения плана.

10.11. Ряд динамики характеризует:

а) структуру совокупности по какому-то признаку;

б) изменения, характеристики, совокупности во времени.

Моментный ряд динамики – это величина показателя;

в) на определённую дату (момент времени);

г) за определённый период времени.

Ответ: 1) а, б; 2) б, в; 3) а, в; 4) -.

10.13. Если сравниваются каждый последующий уровень ряда динамики с предыдущим, то показатели называются:

а) цепными;

б) базисными.

Если сравниваются все уровни ряда с одним уровнем, показатели называются:

в) ценный;

г) базисными

Ответ: 1) а, в; 2) б, в; 3) а, г; 4) б, г.

10.14. Среднегодовой абсолютный прирост равен:

а) разности конечного и начального уровней, делённой на число уровней ряда;

б) базисному абсолютному приросту, делённому на число цепных абсолютных приростов;

в) полусумме конечного и начального уровней.

Ответ: 1) а; 2) б; 3) а, б, в; 4) а, б.

Задачи для решения

Задача 10.1.

Среднегодовая численность рабочих на фирме за 2000-2007 гг. увеличились на 26,5%, в том числе за 2000-2002 гг. на 15%. Определите темп роста среднегодовой численности рабочих за 2002-2007 годы (%).

Задача 10.2.

Темпы прироста объема строительно-монтажных работ, выполненных подрядными организациями города, составили (% к 1995 г.): 2000 г. - 30, 2006 г.. - 89. Определить, как изменился абсолютный прирост объема строительно-монтажных работ, выполненных подрядными организациями за 1995-2006 гг., если стоимость работ в 2006 году составила 630 тыс. грн.

Задача 10.3.

Производство продукции на предприятии в 2004 г. составило 200 тыс. грн. Абсолютный прирост (по сравнению с предыдущим годом) составляет, тыс. грн.: 2005 г. - 46, 2006 г. - 42. Определить среднегодовой темп прироста за 2004-2006 гг., %.

Задача 10.4.

В 1995 г. промышленность страны потребила 22 млрд. кВт. ч электроэнергии, а в 2006 г. - 1,5 раза больше. Определите среднегодовой абсолютный прирост потребления электроэнергии промышленностью страны за 1995-2006 гг.

Задача. 10.5.

Среднегодовая численность рабочих и служащих в народном хозяйстве за 1995-2005 гг. увеличилась на 78%, а численность специалистов с высшим и средним специальным образованием, занятых в народном хозяйстве, в 2 раза. Определите коэффициент опережения роста численности специалистов с высшим и средним специальным образованием, занятых в народном хозяйстве.

Задача 10.6.

За период с 2000 по 2007 гг. численность работающих на заводе увеличилась на 20%. Абсолютное значение 1% прироста - 12 человек. Определите численность работающих в 2007 г.

Задача 10.7.

За ноябрь в списочном составе работников предприятия произошли следующие изменения, чел.: состояло по списку на 1.11. - 919, выбыло с 6.11. - 29; зачислено с 21.11. - 15. Определите среднюю списочную численность работников предприятия за ноябрь, чел.

Задача 10.8.

Грузооборот автомобильного транспорта в стране составил, млн.т км: в 2002 г. - 17,7; в 2007 г. - 21,3. Определите среднегодовой темп роста грузооборота за 2002-2007 годы.

Задача 10.9.

Динамика объёма реализации продукции из регионов характеризуется следующими данными, млн. грн.:

Годы	Варианты
I	II	III	IV	V	VI	VII	VIII	IX	X
Т1	83,2	82,5	82,5	82,8	84,1	83,2	84,2	85,4	82,1	83,4
Т2	91,6	90,0	91,8	91,5	90,0	90,0	92,5	90,8	91,4	90,5
Т3	107,0	106,0	107,7	108,6	108,9	106,1	100,8	107,6	105,4	107,0
Т4	128,5	129,8	129,2	130,3	128,4	128,8	120,0	129,5	128,4	130,4
Т5	163,5	164,1	164,5	165,8	160,1	162,0	158,4	164,0	168,0	168,1
Т6	197,0	198,2	198,9	199,2	196,0	198,4	195,4	196,4	199,2	197,8
Т7	224,4	224,5	224,0	225,3	225,4	224,9	226,7	228,3	229,0	228,4
Т8	269,0	268,0	269,0	271,0	268,0	269,0	270,0	271,0	272,0	271,5
Т9	185,5	290,0	280,0	288,0	295,0	279,0	292,0	290,0	300,5	308,6

Определите показатели динамики цепные и базисные:

1) абсолютные приросты;

2) темпы роста, -

3) темпы прироста,

4) абсолютное значение одного процента прироста;

5) среднегодовые темпы роста и прироста по 5-легиям и за весь период.

Результаты расчетов представить в виде таблицы.

Сделать выводы.

Задача 10.10.

Используя взаимосвязь показателей динамики, определите уровни ряда (добыча угля в стране, млн. т) и недостающие в таблице цепные показатели динамики. Определите среднегодовой абсолютный прирост, темп роста и прироста:

Годы	Добыча нефти, включая газ, конденсат, млн. т	Цепные показатели динамики
Абсолютный прирост, млн. т	Темп роста, %	Темп прироста, %	Абсолютное значение 1% прироста, млн. т
Т1		Х	Х	Х	Х
Т2
Т3			106,1
Т4				7,25
Т5
Т6					4,59
Т7			105,9
Т8				5,0
Т9
Т10					5,72

ТЕМА 11. Анализ тенденций развития

Важной задачей статистики при анализе ряда динамики является определение основной тенденции развития, присущей тому или иному явлению в связи с чем необходимо освоить способы обработки рядов динамики: укрупнение периодов, сглаживание ряда при помощи скользящей средней, аналитическое выравнивание.

Самым простым способом является способ укрупнения периодов (интервалов). Он состоит в расчёте суммарных или средних показателей для увеличенных интервалов. Вместо дневных (годовых) определяют месячные, квартальные, пятилетние и др., однако, надо помнить, что в моментных рядах динамики и в рядах средних величин увеличение интервалов осуществляется только на основе расчёта средних уровней по формуле средней арифметической.

Сглаживание методом скользящей средней заключается в том, что в начале рассчитывается средний уровень с определённого числа первых чисел уровня ряда, затем из того же числа уровней, но начиная со второго, далее – с третьего и т. д. Как правило, определяют среднюю из 3, 5 и более уровней (нечётных).

При аналитическом выравнивании ряда динамики закономерно изменяющийся уровень изучаемого показателя оценивается как функция времени:

y_t = f (t) (11.1)

где y (t) – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основание для выбора вида, кривой может использоваться содержательный анализ сущности развития данного явления. На практике для этих целей прибегают к анализу графического изображения уровней динамического ряда.

Рассмотрим на примере, аналитическое сглаживание ряда динамики объёма экспорта продукции по прямой и параболе.

Пример 11.1. Схема аналитического сглаживания ряда динамики.

Годы	Объём экспорта, импорта, грн (y)	Условные обозначения времени
t	t ^2	t ^4	ty	t ^2 y
Т 1		-9		6 561	- 216	1 944
Т 2		-7		2 401	- 504	3 528
Т 3		-5			- 460	2 300
Т 4		-3			- 306
Т 5		-1			1 114
Т 6
Т 7						1 089
Т 8						3 125
Т 9				2 401		6 027
Т 10				6 561		8 910
Итого				19 338	1 357	28 073

Для вывода уравнения прямой

y = a _{0 +} a ₁ t (11.2)

воспользуемся системой нормальных уравнений:

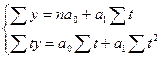(11.3)

где y – фактические уровни ряда динамики.

n – число членов ряда динамики.

Для удобства расчётов отсчёт времени целесообразно вести с середины ряда таким образом, чтобы сумма времён равнялась нулю, т.е. . Если число уровней нечётное, серединное число обозначается 0, предыдущие периоды – отрицательными числами, последующие – положительными.

Если число уравнений динамического ряда чётное, то два серединных момента времени обозначаются – 1 и +1, а другие через два интервала.

При условии Σ t = 0 система уравнений для нахождения a₀ и a, примет вид:

(11.4)

(11.5)

(11.6)

Уравнение тренда по прямой будет иметь вид:

(11.7)

Для вывода уравнения параболы второго порядка:

(11.8)

Необходимо решить систему уравнений:

(11.9)

При условии Σ t = 0, Σ t ³ = 0 система уравнений примет вид:

(11.10)

(11.11)

(как и для прямой)

(11.12)

Подставив данные из таблицы 11.1 получим:

a ₀ = 119,471 a ₁= 4,112 a ₂ = -0,587

Уравнение параболы будет иметь вид:

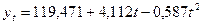(11.13)

Из двух полученных уравнений трендов (11.7 и 11.13) необходимо выбрать наиболее адекватную математическую модель. Для этого рассчитывают ошибку аппроксимации:

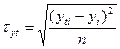(11.14)

где y_ti, y_i – соответственно теоретические и эмпирические уровни ряда.

Расчёт ошибки аппроксимации приведён в таблицу 11.2.

Таблица 11.2

Матрица расчёта ошибки аппроксимации

Годы	ti	yi	Теоретические уровни (yti)	Отклонение теоретических уровней от фактических (yti-yi)^2
прямая	парабола	прямая	парабола
Т1	-9		63,092	34,916	1528,194	119,159
Т2	-7		71,316	61,924	0,468	101,525
Т3	-5		79,54	84,236	155,252	60,279
Т4	-3		87,76	101,852	202,777	0,022
Т5	-1		95,988	114,772	324,432	0,596
Т6			104,212	122,996	190,108	24,96
Т7			112,436	126,524	73,342	30,514
Т8			120,660	125,356	18,836	0.127
Т9			128,884	119,492	34,621	12,306
Т10			137,108	108,932	734,843	1,140
Итого				1000,7	3262,873	350,630

Для прямой:

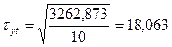
Для параболы второго порядка:

Ошибка аппроксимации ниже y параболы, следовательно, она и будет являться трендом, т.к. предпочтение отдаётся математической модели с минимальной ошибкой.

Вопросы и тесты для самоконтроля

11.1. Какие способы выявления основной тенденции развития явления, Вы знаете?

11.2. В чём заключается сглаживание рядов динамики?

11.3. Как выявляется основная тенденция развития явления - тренд?

11.4. Методы прогнозирования динамики?

11.5. В чём заключается анализ рядов динамики?

11.6. Аналитическое выравнивание позволяет:

а) выявить тенденцию развития;

б) получить качественные характеристики изменения уровней ряда.

Ответы: 1) а; 2) б; 3) а, б; 4) –.

11.7. Тенденция представляет собой изменение ряда динамики:

а) равномерно повторяющееся через определённые промежутки времени внутри года;

б) определяющее какое-то общее направление развития. Сезонные колебания представляют собой изменение ряда динамики равномерно повторяющиеся;

в) через определённые промежутки времени с годичным интервалом;

г) внутри года.

Ответы: 1) а, в; 2) а, г; 3) б, в; 4) б, г.

Задачи для решения

Задача 11.1.

На основе данных задачи 10.10. построить график и произвести аналитическое сглаживание ряда, рассчитав 2 – 3 уравнения тренда и сделать вывод об адекватности модели по ошибке аппроксимации.

Задача 11.2.

На основе данных таблицы 4.3. установить основную тенденцию развития основных показателей работы предприятия, методом укрепления периодов, скользящей средней и аналитическим.

Сделать выводы.

Таблица 11.3

Динамика основных показателей работы предприятия

Период	Объём реали-зации, тыс. грн.	Прибыль, тыс. грн.	Численность работников, чел.	Себестои-мость продукции, грн/шт.	Объём произв-во тыс. шт.
Январь		5,8			0,9
Февраль		3,9			1,1
Март		4,2			1,3
Апрель		5,7			1,5
Май		8,4			1,4
Июнь		9,6			1,8
Июль		10,0			2,0
Август		10,2			2,2
Сентябрь		11,8			2,8
Октябрь		12,5			2,4
Ноябрь		12,9			3,0
декабрь		13,3			3,4

ТЕМА 12. Индексы

При изучении данной темы следует чёток уяснить понятие индексов, как относительного показателя, характеризующего соотношение уровней социально-экономических явлений по времени, по сравнению с планом или в пространстве.

Необходимо усвоить символику (условные обозначения), применяемую при использовании индексного метода, т.к. она применяется и в статистике, и в экономике отрасли:

Q – количество произведенной продукции данного вида в натуральном выражении;

T – общие затраты рабочего времени на производство продукции данного вида (чел/часы, чел/дни);

S – себестоимость единицы продукции;

Ц – цена единицы продукции;

- производство продукции данного вида в единицу времени (либо выработка на 1 работника);

- затраты рабочего времени на производство единицы продукции, т.е. трудоемкость;

S Q – общая себестоимость продукции данного вида (общие затраты на производство)

Ц Q – общая стоимость произведенной продукции данного вида (выручка от реализации, товарооборот)

Все индексируемые показатели могут быть двоякого рода: качественными интенсивными (выработка, себестоимость, цена) и количественными-экстенсивными (объем продукции данного вида, численность рабочих, общая себестоимость продукции и др.).

По охвату элементов совокупности следует различать индексы индивидуальные (элементарные) и сводные (сложные). Индивидуальный индекс (i) характеризует соотношение уровней только одного элемента совокупности:

- индекс цен:

(12.1)

где Ц_1, Ц₀ – цена отчетного и базисного периодов.

- индекс себестоимости:

(12.2)

Дата добавления: 2015-07-12