Способ. 2 страница

При небольшом числе наблюдений исследовать влияние одного или нескольких факторных признаков на результативный можно, используя методы дисперсионного анализа.

Дисперсионный анализ проводится путем расчета дисперсий: общей, межгрупповой, внутригрупповой.

Общую дисперсию (σ²_y) называют дисперсией комплекса, межгрупповую (σ²_F) - факторной, внутригрупповую (σ²_о) – остаточной.

Дисперсионный анализ заключается в сравнении факторной и остаточной дисперсий. Если различие между ними значимо, то факторный признак, т.е. признак, положенный в основание группировки, оказывает существенное влияние на результативный. При исследовании воздействия на результативный признак только одного факторного признака дисперсии исчисляются по следующим формулам:

- дисперсия комплекса:

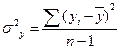(7.4)

- факторная дисперсия:

(7.5)

- остаточная дисперсия:

(7.6)

На основании дисперсий производится расчет критерия Фишера (F). Если расчетное значение F_p, больше табличного, т.е. F_p>F_a, то существенность влияния факторного признака подтверждена.

(7.7)

Пример 7.2. При изготовлении одной из деталей были предложены три вида технологии ее обработки: устаревшая, обычная и прогрессивная. Для выбора наиболее экономичного способа обработки с помощью каждой из них было изготовлено по нескольку деталей. Данные на обработку одной детали следующие:

Технология изготовления	Число деталей	Время на обработку одной детали, мин.
1. Прогрессивная		4,3; 5,2; 6,1; 4,7; 7,0
2. Обычная		6,0; 6,8; 7,9; 8,4; 5,1; 4,9; 9,0
3. Устаревшая		8,4; 7,9; 10,2; 11,4; 12,8; 6,2; 13,6; 15,0
Итого

Нужно определить, значительно ли различаются между собой эти способы обработки?

Рассчитаем среднее время обработки одной детали по различным технологиям по формуле простой среднеарифметической.

мин. мин. мин.

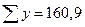
= 18,49 +27,04+…+36,0+46,24+…+70,56+…+225 = 1479,27

Найдем:

- общую сумму квадратов отклонений:

-

- сумму межгрупповых квадратов отклонений:

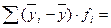(5,46-8,05)^2.5+(6,87-8,05)^2.7+(10,69-8,05)^2.8= 99,04

- факторную дисперсию:

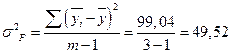
- остаточную сумму квадратов:

184,83 - 99,04 = 85,79

Определим остаточную дисперсию:

Рассчитаем критерий Фишера

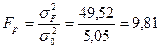при Р = 0,99

т.е. >

Следовательно, затраты времени на обработку деталей, существенно различны. Признак, положенный в основание группировки «Технология изготовления», оказывает существенное влияние на время обработки одной детали.

Вопросы и тесты для самоконтроля

7.1. В чем состоит связь между корреляционной и функциональной связью?

7.2. Какие основные проблемы решает исследователь при изучении корреляционных зависимостей?

7.3. Какова роль групповых и корреляционных таблиц при анализе взаимосвязи?

7.4. Из приведенных зависимостей корреляционными являются:

а) заработная плата и стаж работы;

б) заработная плата и цена реализуемой продукции.

Ответ: 1) а; 2) б; 3) а,б; 4) -.

7.5. Корреляционное отношение используется для оценки тесноты связи, если вариационными признаками являются:

а) только результативный признак;

б) только факторный признак;

в) оба признака.

Ответ: 1) а; 2) б; 3) в; 4) -.

7.6. Если факторный признак описательный, а результативный количественный, то для анализа взаимосвязи между ними используются:

а) аналитическая группировка;

б) уравнение регрессии;

в) дисперсионный анализ.

Ответ: 1) а; 2) а,в; 3) а,б; 4) а,б,в.

7.7. Если коэффициент детерминации ŋ ² = 0 это означает:

а) значения вариант в пределах групп одинаковы;

б) связь отсутствует;

в) связь функциональная;

г) расхождение между групповыми средними отсутствует.

Ответ: 1) а,б; 2) а,г; 3) б,в; 4) б,г.

Задачи для решения

Задача 7.1.

Статистическая совокупность разбита по факторному признаку на 4 группы с порядковыми номерами 1, 2, 3, 4. Рассчитаны следующие показатели по результативному признаку:

1) общая средняя величина его в совокупности равна 22,8 единиц его размерности;

2) групповые средние: х ₁ = 20, х _{2 = 25,} величина средней третьей группы не известна, ее надо определить, х ₄ = 22.

3) средние квадратические отклонения: σ₁ = 10, σ₂ = 5, σ₃ = 6, σ₄ = 7;

4) численность единиц (n) в группах: n₁ = 30, n₂ =30, n₃ = 25, n₄ = 15.

Определите корреляционное отклонение. Сделайте выводы.

Задача 7.2.

На основе исходных данных задачи 4.18 выполнить перегруппировку исходных данных, образовав 2 – 3 группы рабочих по уровню их квалификации (например: низкая, средняя, высокая) и установить степень взаимосвязи между уровнем их квалификации рабочих и их производительностью труда.

Сделать выводы.

Задача 7.3.

На основе данных задачи 3.1 методом дисперсионного анализа установить взаимосвязь и рассчитать тесноту взаимосвязи:

1) заработной платы от стажа работы;

2) заработной платы от производительности труда;

3) производительности труда от стада работы.

Сделать выводы.

Задача 7.4.

По данным опроса 100 женщин выявлена зависимость возрастом вступления их в брак и продолжительностью брачных отношений:

Возраст вступления в брак	Количество женщин	Средний срок длительности брачных отношений, лет
Ранний
Младший
Средний
Итого

Общая дисперсия продолжительности брачных отношений составляет 16.

Определить межгрупповую дисперсию и корреляционное отношение. Сделать выводы.

Задача 7.5.

Вычислите корреляционное отношение, характеризующее тесноту связи между возрастом оборудования и процентом выполнения норм выработки рабочими-сдельщиками на этом оборудовании.

Возраст оборудования, лет	Число станков, шт.	Выполнение норм, %	Внутригрупповая дисперсия
1-3
3-7
7-12
12 и выше
Всего		-	-

Проверьте существенность связи с помощью F – критерия Фишера при Р = 0,95.

Задача 7.6. Методом дисперсионного анализа по условию задачи 3.1. найти зависимости:

1) заработной платы от стажа работы;

2) заработной платы от производительности труда;

3) производительности труда от стажа работы.

При расчете межгрупповой и общей дисперсии необходимо использовать результаты проведенных соответствующих аналитических группировок и расчетов. Следует сделать выводы о значимости каждого из факторов и достоверности его влияния на соответствующий результат.

ТЕМА 8. Анализ таблиц взаимной сопряженности

В некоторых случаях в экономико-статистических исследованиях для установления взаимосвязи используются признаки, которые не имеют числового выражения (атрибутивные признаки), поэтому приходится прибегать к использованию непараметрических методов. Эти методы позволяют измерить интенсивность связи как между количественными признаками, форма распределения которых отличается от нормальной, так и между качественными признаками. В основу непараметрических методов положен принцип нумерации значений статистического ряда. Каждой единице совокупности присваивается порядковый номер в ряду, который будет упорядочен по уровню признака. Таким образом ряд значений признака ранжируется, а номер каждой отдельной единицы будет ее рангом.

Коэффициенты корреляции, основанные на использовании рангов были предложены К. Спирменом и М. Кендэлом.

Коэффициент корреляции рангов (К_с) (коэффициент Спирмена) рассчитывается по рангам взаимосвязанных признаков следующим образом:

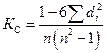(8.1)

где d²_i – квадраты разности рангов;

n – число наблюдений (число пар рангов).

Коэффициент знаков (К_ф) (коэффициент Фехнера) вычисляется на основании определения знаков отклонений вариантов двух взаимосвязанных признаков от их средней величины:

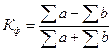(8.2)

где a – число совпадений знаков;

b – число несовпадений знаков.

Для определения тесноты связи между тремя и более признаками применяется ранговый коэффициент согласия - коэффициент конкордации (К_к).

(8.3)

где m – количество факторов;

n – число наблюдений;

S – сумма квадратов отклонений рангов.

При исследовании социальных явлений и процессов большое значение имеет изучение качественных показателей и процессов большое значение имеет изучение качественных показателей и признаков, не имеющих количёственной оценки:

a	b	a+b
c	d	c+d
a+c	b+d	a+b+c+d

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп применяются коэффициенты ассоциации (А) и контингенции (К):

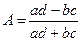(8.4)

(8.5)

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если А ≥ 0,5, К ≥ 0,3.

Если каждый из качественных признаков состоит более, чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона.

Пример 8.1. Располагая данными о результатах обучения рабочих на курсах повышения квалификации и их производительности труда, составим следующую таблицу:

Группы рабочих	Производительность труда по сравнению с предыдущим периодом	всего
не изменилась и выросла	снизилась
Повысившие квалификацию	200(а)	40(в)
Не прошедшие повышение квалификации	46(с)	34(d)
Всего

Коэффициент ассоциации:

Коэффициент контингенции:

Результаты расчетов показали наличие связи между изучаемыми признаками.

В качестве критерия наличия связи между качественными показателями с большим числом градаций можно использовать критерий «ХИ - квадрат»:

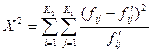(8.1)

где и - соответственно эмпирические и теоретические частоты в i – й строке j – столбца.

К ₁ и К ₂ - соответственно число групп в строках и столбцах таблиц.

На основе критерия «ХИ - квадрат» определяются показатели степени тесноты связи: коэффициенты взаимной сопряженности К.Пирсона и А.А.Чупрова.

Коэффициент взаимной сопряженности К.Пирсона определяется по формуле:

(8.2)

где n – общее число наблюдений.

Коэффициент взаимной сопряженности А.А.Чупрова:

(8.3)

Чем выше коэффициент сопряженности, тем связь между признаками теснее.

Вопросы для самоконтроля

8.1. Какие методы целесообразно использовать для выявления возможного наличия связи между факторным и результативным признаком при небольшом объеме фактических данных?

8.2. Какие показатели являются мерой тесноты связи между двумя признаками?

8.3. Какие показатели используют для измерения степени тесноты связи между качественными признаками?

8.4. Как оценивается теснота связи между альтернативными признаками?

8.5. В каких случаях целесообразно использование таблиц взаимной сопряженности?

8.6. Ранговый коэффициент корреляции используется для оценки тесноты связи между:

а) количественными признаками;

б) признаками, значения которых можно упорядочить;

в) атрибутивными признаками.

Ответ: 1) а; 2) а,в; 3) б; 4) а,в.

8.7. Для оценки тесноты связи между альтернативными признаками можно использовать:

а) коэффициент взаимной сопряженности;

б) коэффициент ассоциации;

в) критерий Х ².

Ответ: 1) а; 2) а,б; 3) а,б,в; 4) в.

Задачи для решения

Задача 8.1.

Методом ранговой корреляции установить степень тесноты связи между уровнем механизации и трудоемкостью изготовления продукции.

Сделать выводы.

№ предприятия
уровень механизации, %
трудоемкость продукции, мин

Задача 8.2.

Определите тесноту связи с помощью коэффициента знаков Фехнера между среднегодовой стоимостью основных производственных фондов и долей ручных работ по 10 однотипным предприятиям.

Номер предприятия
Среднегодо-вая стоимость основных производ-ственных фондов, млн. грн	20,6	8,9	32,7	10,2	28,4	12,4	26,4	11,7	50,9	6,4
Доля ручных работ, %	18,6	36,5	40,4	18,9	22,7	28,6	34,2	21,6	19,7	26,2

Задача 8.3

На основе данных распределения предприятий отрасли по техническому и организационному уровню развития, предусматриваемых в таблице, установить наличие связи по критерию «ХИ - квадрат» и определить показатели степени тесноты связи (коэффициенты сопряженности Пирсона и Чупрова). Сделать выводы.

Распределение предприятий отрасли по техническому и организационному уровню развития.

Группы предприятий по техническому уровню	Группы предприятий по организационному уровню	Итого
ниже среднего уровня	среднего уровня	выше среднего уровня
Ниже среднего уровня
Среднего уровня
Выше среднего уровня
Итого

ТЕМА 9. Статистические методы анализа корреляционных связей

Изучение корреляционных связей производится рассмотренными ранее методами аналитических группировок в комплексе со средними величинами и методом дисперсионного анализа. Более глубоким является регрессионно-корреляционный анализ (РКА).

Первым этапом корреляционного анализа является установление причинной обусловленности связей между изучаемыми признаками. Вторым – отбор наиболее существенных признаков и установленные формы связи (коэффициентов регрессии и корреляции) и завершающим этапом является статистическая оценка показателей связи, полученным по выборочным совокупностям.

Связь между двумя факторами аналитически выражается уравнениями, а для определения параметров этой связи пользуются системами нормальных уравнений.

Для прямой:

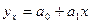(9.1)

Система нормальных уравнений:

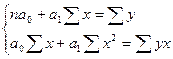(9.2)

Для гиперболы:

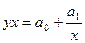(9.3)

Система уравнений:

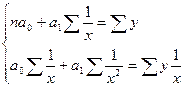(9.4)

Для параболы:

(9.5)

Система уравнений:

(9.6)

Параметр а ₀ показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов. Параметр а ₁ – коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу. На основе этого параметра вычисляются коэффициенты эластичности (Э), которые показывают изменение результативного признака в процентах в зависимости от изменения факторного признака на 1%.

(9.7)

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:

(9.8)

При криволинейной зависимости с помощью корреляционного отношения:

(9.9)

Пример 9.1. По данным о стоимости основных производственных фондов и объеме валовой продукции нужно определить уравнение связи и тесноту связи.

Стоимость основных произведственных фондов, млн. грн (Х)	Объем продукци, млн. грн. (У)	Расчетные графы
XY	X^2	Y^2	YX
					19,4
					25,0
					30,6
					36,2
					41,8
					47,4
					53,0
					58,6
					54,2
					69,8
∑=55	∑=445	∑=2907	∑=385	∑=22487	∑=446

Проанализировав исходные данные, можно предположить, что связь линейная. Принимая для этой вязи уравнение прямой линии (9.1) определим его параметры на основе метода наименьших квадратов, решив систему уравнений (9.2).

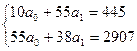
а ₀ = 13,8 а ₁ = 5,6 у_х = 13,8 + 5,6 х

Следовательно, с увеличением стоимости основных производственных фондов на 1 млн. грн объем валовой продукции увеличивается в среднем на 5,6 млн. грн или с увеличением стоимости основных производственных фондов на 1 % объем валовой продукции увеличивается на 0,69 %.

Рассчитаем величину линейного коэффициента корреляции

Величина коэффициента корреляции (0,98) свидетельствует о тесной связи между изучаемыми признаками.

Показателем значимости и полезности прямой, выражающей соотношения между двумя признаками, служит средняя квадратическая ошибка уравнения регрессии (S_е).

(9.10)

где y_i, y_{i, x} – соответственно фактические и рассчитанные по уравнению регрессии значения результативного признака;

m – число параметров в уравнении регрессии.

Средняя квадратическая ошибка уравнения даёт нам возможность в каждом отдельном случаи с определённой вероятностью указать, что величина результативного признака окажется в определённом интервале относительно значения, вычисленного по уравнению связи.

Вопросы и тесты для самоконтроля

9.1. В чем сущность регресионно-корреляционного анализа и каковы его этап?

9.2. Какое различие между прямой и обратной линейной и криволинейной связями?

9.3. Какой метод используется при нахождении параметров уравнения регрессии?

9.4. Какие задачи статистико-экономического анализа решают с помощью уравнения регрессии?

9.5. Какие признаки можно включать в уравнение регрессии?

9.6. От чего зависит функциональный вид линейного уравнения регрессии?

9.7. Экономический смысл параметров линейного уравнения регрессии.

9.8. Можно ли измерить тесноту связи по уравнению регрессии? Особенность такого измерения.

9.9. Экономический смысл параметров многофакторного линейного уравнения регрессии. Чем они отличаются от параметров однофакторных линейных уравнений?

9.10. Коэффициент корреляции между производительностью труда рабочих и стажем их работы составляет + 0,88. Это означает, что:

а) связь прямая;

б) связь обратная;

в) связь существенная;

г) связь несущественная

Ответ: 1) а, в; 2) а, г; 3) б, в; 4) б, г.

Задачи для решения

Задача 9.1.

По приведенным данным методом регресионно-корреляционного анализа найти зависимость производительности труда рабочих от фондовооруженности. Для этого исчислите коэффициенты регрессии, корреляции. Установите достоверность полученных характеристик связи.

Сделайте выводы.

Заводы	Фондовооруженность рабочих, тыс. грн	Производительность труда, тыс. грн
	9,25	10,4
	10,30	12,2
	15,20	27,2
	8,42	10,1
	13,21	17,2
	7,58	8,0
	4,50	3,9
	11,20	16,0
	10,00	12,3
	3,56	4,4

Задача 9.2.

Методом дисперсионного анализа по условию задачи 3.1 найти зависимости:

1) заработной платы от стажа работы;

2) заработной платы от производительности труда;

3) производительности труда от стажа работы.

Сделайте выводы.

Задача 9.3.

Найти зависимость между выпуском продукции и объёмом основных фондов в виде уравнения линейной регрессии. Определить тесноту взаимосвязи с помощью линейного коэффициента корреляции.

Стоимость основных призводственных фондов, млн. грн.
Объём выпущенной продукции, млн. грн.	3,8	4,6	6,3	5,8	7,6	8,4	7,0	5,2

Задача 9.4.

По данным задачи 8.1 найти уравнение регрессии, описывающее изменение трудоёмкости продукции при изменении уровня механизации производственных процессов. Рассчитать тесноту связи между изучаемыми признаками.

ТЕМА 10. Анализ интенсивности динамики

В данной теме необходимо изучить основные понятия о рядах динамики и четко представлять себе их виды. В зависимости от того, выражают ли уровни ряда состояние явления на момент времени или его величину за определенные периоды времени, различают соответственно моментные и интервальные ряды.

В зависимости от способов выражения уровней, ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.

Дата добавления: 2015-07-12