Способ. 1 страница

Способ моментов основан на отсчете от условного начала (нуля):

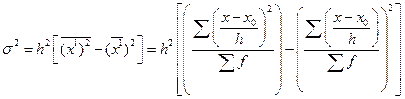(5.17)

Условные обозначения в этой формуле и методика расчета значений новых вариант та же, что в формуле (4.12).

Используя данные предыдущего примера, рассчитываем дисперсию тарифных разрядов слесарей методом моментов.

За х_о принимаем значение варианты, расположенной в середине ряда (х_о=4), h=1, тогда

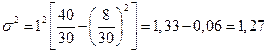
Важной задачей при анализе совокупности является определение формы кривой распределения. Качественно однородные совокупности имеют одновершинную форму, которая может быть симметричной, асимметричной, островершинной или плосковершинной. Для сравнительного анализа степени асимметрии рассчитывают коэффициент асимметрии (А):

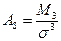(5.18)

где 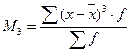- центральный момент 3-го ряда (5.19)

Если 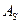> 0, т.е. 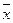> Ме > Мо, то асимметрия является положительной со смещением влево. Если 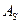< 0, т.е. 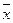< Ме < Мо, то асимметрия является отрицательной со смещением вправо.

Показателем островершинности служит коэффициент эксцесса ()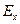

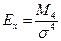(5.20)

где 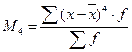- центральной момент 4-ого порядка (5.21)

При 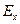= 3 – нормальное распределение; 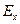> 3 – островершинное; 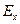< 3 – плосковершинное.

Вопросы для самоконтроля

5.1. Что такое мода и медиана?

5.2. В каких случаях применение моды и медианы предпочтительнее средней арифметической?

5.3. Назовите структурные средние в статистике.

5.4 Что такое вариация признаков?

5.5. Как следует понимать закономерность распределения? Можно ли ее количественно измерить?

5.6. По какой формуле целесообразно рассчитывать дисперсию, если средняя - дробное число, например, 2,687?

5.7 Можно ли сравнить вариации двух признаков, имеющих разное качественное выражение?

5.8. Изменится ли дисперсия, если все значения признака разделить (умножить) на одну и ту же величину?

5.9. Как определяется дисперсия альтернативного признака?

5.10. Какие Вы знаете показатели измерения вариации признаков?

5.11. Что показывает коэффициент вариации и для какой цели его рассчитывают?

5.12. Чем характеризуется ряд распределения?

5.13. Что представляет собой кумулятивный ряд?

5.14. Что показывают коэффициенты асимметрии и эксцесса?

5.15. Среднее значение признака у двух совокупностей одинаково. Может ли быть разной вариация признака в этих совокупностях?

а) да;

б) нет.

Среднее значение признака у двух совокупностей разное. Может ли быть одинаковой вариация признака в этих совокупностях?

в) да;

г) нет.

Ответ: 1) а,в; 2) а,г; 3) б,в; 4) б,г.

5.16. Дисперсия представляет собой:

а) средний размер отклонений вариант от средней;

б) средний квадрат этих отклонений.

Она может быть рассчитана:

в) только для количественного признака;

г) для количественного и альтернативного признака.

Ответ: 1) а,в; 2) а,г; 3) б,в; 4) б,г.

5.17. Идентичны ли по содержанию среднее линейное и среднее квадратическое отклонения?

а) да;

б) нет.

Равны ли они по абсолютной величине?

в) да;

г) нет.

Ответ: 1) а,в; 2) а,г; 3) б,в; 4) б,г.

Задачи для решения

Задача 5.1.

Распределение рабочих 3-х предприятий одного объединения по тарифным разрядам характеризуется следующими данными:

Тарифный разряд	Численность рабочих на предприятиях
№1	№2	№3

Определите по каждому предприятию:

1) средний тарифный разряд рабочих;

2) моду, медиану, квартили тарифных разрядов;

3) все показатели вариации;

4) коэффициенты асимметрии и эксцесса.

Сделайте выводы.

Задача 5.2.

По данным задачи 4.18 выполнить полный анализ ряда распределения, определив:

1) структурные средние (моду, медиану, квартили);

2) показатели вариации (размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициенты вариации);

3) форму кривой распределения (коэффициенты асимметрии и эксцесса);

Сделать выводы.

Задача 5.3.

По результатам группировки, выполненной в задаче 4.17 рассчитать:

1) структурные средние;

2) показатели вариации;

3) установить форму распределения.

Сделать выводы.

Задача 5.4.

Если все частоты признака увеличить в 5 раз, а значения каждого признака уменьшить в 5 раз, как изменятся показатели?

1) средняя;

2) дисперсия;

3) коэффициент вариации.

Задача 5.4.

Дисперсия признака равна 81, средний квадрат индивидуальных значений его 250. Чему равна средняя арифметическая?

Задача 5.5.

Дневная выработка деталей токарями одной бригады составила 10, 12, 13, 17 шт., дисперсия 1,69. Определить коэффициент вариации выработки.

Задача 5.6.

Коэффициент вариации признака равен 40%. Чему будет равен коэффициент вариации, если все варианты уменьшить в 10 раз?

Задача 5.7.

Распределение семей в области по числу детей характеризуется следующими данными:

Число детей								Итого
Доля семей, % к итогу

Используя показатели асимметрии и эксцесса, сделайте выводы о форме распределения изучаемой совокупности семей.

Задача 5.8.

По размеру среднесуточной производительности агрегатов цехи распределились следующим образом:

Среднесуточная производительность агрегатов, тыс. т	-	-	-	10-12	12-14	14-16	16-18	18-20		Итого
Число цехов

Используя функцию нормального распределения, определите теоретические частоты распределения цехов по среднесуточной производительности станов и с помощью критерия Колмогорова (χ²) проверьте, согласуется ли оно с нормальным распределением. Выводы сделайте с вероятностью 0,90.

Задача 5.9.

По данным группировки задачи 3.1 определите теоретические частоты распределения предприятий по численности работающих, соответствующее нормальному распределению, и с помощью критерия χ² проверьте существенность значений между теоретическими и эмпирическими частотами. Выводы сделайте с вероятностью 0,95.

ТЕМА 6. Выборочный метод

При изучении данной темы необходимо усвоить сущность выборочного наблюдения, его преимущества и недостатки перед сплошным наблюдением, а также область применения.

Необходимо разобраться в основных видах отбора (собственно-случайный, механический, типический, серийный, комбинированный), уяснить условия применения каждого из них.

Очень важным моментом в изучении данной темы является закрепление теоретического материала и решения задач по определению предела случайной ошибки репрезентативности для различных типов выборочных характеристик и определение объема выборки, обеспечивающей необходимую репрезентативность выборочной совокупности.

Ошибка репрезентативности, или разность между выборочной и генеральной характеристикой, рассчитывается как предел наивероятной ошибки. В качестве уровня гарантийной вероятности (Р) обычно берется 0,954 или 0,997. Тогда предел ошибки (Δ) обычно определяется величиной удвоенной или утроенной средней ошибки выборки (μ):

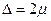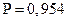
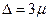при

при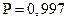

или в общем виде:

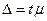(6.1)

где t – коэффициент, связанный с вероятностью, гарантирующей результат. Следует помнить, что величина средней ошибки выборки различна для отдельных видов отбора.

При собственно случайном и механическом повторном индивидуальном отборе средняя ошибка выборки:

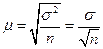(6.2)

-предельная ошибка выборки:

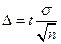(6.3)

где, σ² – общая дисперсия признака;

n – число отобранных единиц наблюдения.

ω – средняя ошибка доли:

(6.4)

При серийном, повторном отборе:

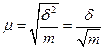(6.5)

При бесповторном, серийном отборе:

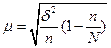(6.6)

При собственно-случайном и механическом бесповторном отборе средняя ошибка выборки:

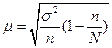(6.7)

- средняя ошибка доли:

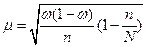(6.8)

При типическом повторном отборе:

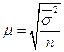(6.9)

При типическом бесповторном отборе:

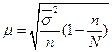(6.10)

Для решения практических задач пользуются предельной ошибкой выборки.

Пример 6.1. С вероятностью 0,954 нужно определить границы среднего веса детали, если контрольная выборочная проверка дала следующие результаты (первые 2 графы таблицы).

Вес 1 детали, г (х)	Количество деталей (f)	Расчетные графы
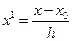х0=49,5
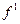
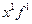
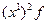
48-49		-1		-2
49-50
50-51		+1
51-52
Итого

Средний вес детали по выборке:

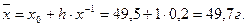
Выборочная дисперсия веса 1 детали:

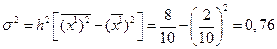
Средняя ошибка выборочной средней:

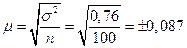г.

Предел для ошибки с вероятностью 0,954:

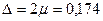
Границы генеральной средней:

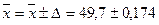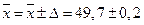г

г

Таким образом с вероятностью 0,954 можно утверждать, что в среднем вес детали для всей партии не более 49,74 и не менее 49,526 г.

Если бы в условии предыдущей задачи было сказано, что выборка бесповторная составляет 20% генеральной совокупности, то в этом случае необходимо сделать поправку на данный вид отбора.

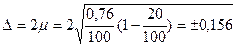
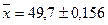г.

Необходимая численность выборки определяется на основе формул предельной ошибки выборки:

- для собственно-случайного и механического отбора:

- выборка повторная:

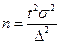(6.11)

- для доли:

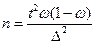(6.12)

- выборка бесповторная:

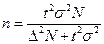(6.13)

- для доли:

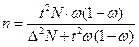(6.14)

Пример 6.2. В цехе работает 2500 человек. Определить численность выборки для контроля среднегодовой производительности труда рабочих при условии повторного отбора и бесповторного отбора. Коэффициент доверия t = 2 (Р = 0.954). Предельная ошибка выборки при определении среднегодовой производительности труда составляет 20 т/чел, среднее квадратическое отклонение σ = 300 т.

1) Численность выборки для повторного отбора:

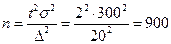чел

2) Для бесповторного отбора:

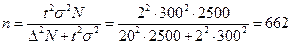чел

Т е. для получения предельной ошибки выборки не более 20 т/чел при σ =300 т и t = 2 необходимо отобрать 900 рабочих при повторной выборке и 662 рабочих при бесповоротной выборке.

Вопросы и тесты для самоконтроля

6.1. Что представляет собой выборочное наблюдение?

6.2. В чем заключаются условия проведения выборочного наблюдения?

6.З. Какие существуют виды отбора?

6.4. Какие существуют методы отбора?

6.5. Почему определяется средняя из возможных ошибок выборки?

6.6. В чем состоят особенности выборочного наблюдения? -

6.7. Что представляют собой ошибки репрезентативности?

6.8. Охарактеризуйте методы расчета средней из возможных ошибок выборочного наблюдения.

6.9. Как определяется необходимая численность выборки?

6.10. Охарактеризуйте способы распространения выборочных данных на генеральную совокупность.

6.11. Случайная ошибка репрезентативности возникает вследствие:

а) нарушения принципов случайности отбора;

б) несплошного характера наблюдений.

Можно ли избежать случайной ошибки репрезентативности?

в) да;

г) нет.

Ответ: 1) а,в; 2) а,г; 3) б,а; 4) б,г.

6.12. Средняя ошибка выборки определяется с целью:

а) изучения вариации признака;

б) изучения среднего значения изучаемого признака;

в) изучения коэффициента роста;

г) установления возможных пределов отклонений генеральной от средней выборочной.

Ответ: 1) а,в; 2) а,г; 3) б,а; 4) б,г.

6.13. По данным выборочного наблюдения (5 % выборка) удельный вес продукции, переведенной во второй сорт, на первом предприятии составила 5 %, а на втором – 6 %. При одинаковом объеме выборки, ошибка выборки для продукции, переведенной во второй сорт:

а) больше на первом предприятии;

б) больше на втором предприятии;

в) ошибки одинаковы;

г) предусмотреть нельзя.

Ответ: 1) а; 2) б; 3) в; 4) г.

6.14. Чтобы уменьшить среднюю ошибку выборки в 2 раза, необходимо объем случайной выборки:

а) увеличить в 2 раза;

б) увеличить в 4 раза;

в) уменьшить в 2 раза;

г) уменьшить в 4 раза.

Ответ: 1) а; 2) б; 3) в; 4) г.

Задачи для решения

Задача 6.1.

С целью контроля за наблюдением норм расхода сырья проведено выборочное обследование партии заготовок деталей. При механическом бесповторном отборе 2% изделий, поступающих из литейного цеха, получены следующие данные о распределении образцов по весу:

Вес изделия, г	Число деталей
до 1000
1000-1025
1025-1050
1050-1075
1075-1100
1100 и выше
Итого

Норма расхода сырья на заготовку - 1050 т Проверьте, соответствует ли фактический расход сырья установленной норме.

Выводы сделайте с вероятностью 0,997.

Задача 6.2.

Для изучения производительности труда рабочих было проведено десятипроцентное выборочное наблюдение (механический способ отбора) в результате которого получено следующее распределение рабочих по дневной выработке.

Дневная выработка, т	до 60	60-80	80-100	100-120	120 и >	Всего
Число рабочих, чел

По выборочной совокупности исчислить среднюю выработку рабочих и с вероятностью 0,997 определить возможные пределы, в которых находится средняя производительность труда рабочих на участке.

Задача 6.3.

Укажите способы формирования выборочной совокупности при изучении:

1) продолжительности срока службы металлорежущих станков, если отбирался каждый третий завод министерства и на попавших в выборку заводах подвергались обследованию все металлорежущие станки;

2) среднего количества слов в телеграмме, если отбиралась каждая сотая телеграмма;

3) средней выработки рабочих, если отбирался каждый пятый среди специализированных цехов, а внутри цехов проводилось сплошное обследование;

4) потерь рабочего времени на участке, если через каждый час в карте наблюдения фиксировалось, чем заняты рабочие;

5) бюджета времени работающих, если отбиралось, каждое пятое предприятие из их общего списка по отрасли промышленности, а на отобранных предприятиях - каждый сотый рабочий или служащий.

Задача 6.4.

По приведенным данным пятипроцентного выборочного обследования (способом механического отбора) выполнения норм выработки рабочими цеха, определить:

а) средний процент выполнения норм выработки;

б) моду;

в) медиану;

г) с вероятностью 0,997 пределы, в которых ожидается средний процент выполнения нормы выработки по цеху;

д) с вероятностью 0,954 - возможные пределы доли рабочих, выполняющих нормы выработки на 120’% и более.

Сделать выводы.

Выполнение нормы выработки, %	Численность рабочих, чел
до 90
90-100
100-110
110-120
120 и более

Задача 6.5.

На основе данных задачи 5.3. найти пределы в которых находится значение изучаемого признака в генеральной совокупности (с вероятностью 0,954).

Задача 6.6.

По данным выборочного обследования (20-процентный отбор) доля жителей города старше 60 лег составляет 10 %, в возрасте до 16 лет - 14%. доля рабочих (без числа членов их семей) - 18%. Обследовано 400 человек с вероятностью 0,954 определите возможные пределы значений показателей в - генеральной совокупности.

Задача 6.7.

С целью определения затрат времени на изготовление детали проведен хронометраж работы 25 рабочих, отобранных в случайном порядке (каждый десятый рабочий). По данным выборки получила х = 15 мин. при σ² = 2 мин.

Определить:

а) как изменится ошибка выборки если объем выборочной совокупности увеличить в 2 раза?

б) как скажется на ошибке выборки увеличение дисперсии в 1,5 раза?

в) как изменятся ошибка выборки, если с увеличением дисперсии в 1,5 раза объем выборочной совокупности увеличить в 2,5 раза?

ТЕМА 7. Статистические методы изучения связи

Изучение взаимосвязей социально-экономических явлений – важнейшая задача статистики. Прежде всего необходимо усвоить сущность функциональной и стохастической связи, а также особенности проявления и необходимость изучения корреляционной связи.

Как было отмечено ранее в теме 3, метод аналитической подстановки дает возможность установить взаимосвязь между изучаемыми признаками. Однако, установив эту взаимосвязь, необходимо установить, какую роль играет исследуемый фактор в изменении результативного признака и является ли он главенствующим. Эту задачу решают с помощью измерения тесноты связи, в основе которого лежит правило сложения дисперсий.

Если статистическая совокупность разбита на группы по какому-либо признаку, то средняя величина и дисперсия признака могут быть определены не только для всей совокупности, но и для каждой из составляющих ее групп. Наряду с групповыми дисперсиями может быть найдено и среднее ее значение ():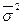

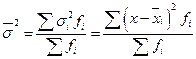(7.1)

Межгрупповая дисперсия (δ²) служит мерой колеблемости групповых средних (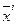) около общей средней ():

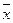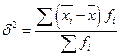(7.2)

Общая дисперсия складывается из внутри- и межгрупповой дисперсий (правило сложения дисперсий):

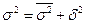(7.3)

Если окажется, что 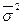= 0, то δ² = σ², а отношение межгрупповой дисперсии к общей равно единице. Это позволяет полагать, что никакие прочие факторы не оказывают влияния на результативный признак, что вся вариация его обусловлена действием на него признака - фактора, положенного в основание группировки и следовательно, между этими признаками очень тесная связь.

Если δ² = 0, то можно утверждать, что связь между изучаемыми признаками почти или полностью отсутствует. Отношение межгрупповой дисперсии к общей позволяет судить о связи между изучаемыми признаками и называется коэффициентом детерминации (η²):

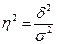
Однако, чаще всего в качестве показателя тесноты связи используют корреляционное отношение (эмпирическое) (η):

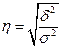
Пример 7.1. Вычислим все дисперсии по следующим данным о распределении рабочих цехов по среднедневной производительности труда:

Номер цеха	Производительность труда, т/чел	Числен-ность рабочих, чел.	f	xf	x^2	x^2f
Итого

Для упрощения вычислений сократим численность работающих в 50 раз (используя свойства средней).

Средняя производительность труда:

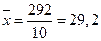т/чел

Общая дисперсия:

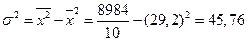
Производительность труда зависит от многих факторов (уровень механизации и автоматизации, условия работы, квалификация рабочих, условия оплаты труда и др,). Общая дисперсия в данном случае измеряет колеблемость производительности труда за счет всех этих факторов.

Разобьем нашу совокупность на 2-группы:

I группа (1-3 цехи) цехи с низким уровнем механизации и автоматизации производственных процессов.

II группа (4-6 цехи) - цехи со средним уровнем механизации и автоматизации производственных процессов.

При такой группировке производительность труда будет результативным признаком.

Определяем:

1) групповую среднюю:

- для I группы т/чел

- для II группы 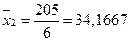т/чел

2) средний квадрат вариантов признака:

- для I группы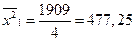

- для II группы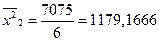

3) дисперсию:

- для I группы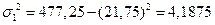

- для II группы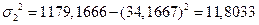

4) среднюю из групповых дисперсий:

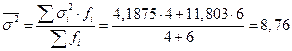
5) межгрупповую дисперсию:

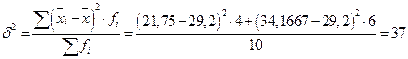
6) общую дисперсию:

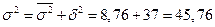
7) коэффициент детерминации:

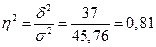
8) корреляционное отношение:

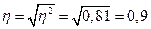
Это свидетельствует о том, что степень автоматизации и механизации производственных процессов в цехах существенным образом влияет на производительность труда рабочих.

Дата добавления: 2015-07-12