Электрооптические эффекты

Продольный линейный электрооптический эффект (эффект Поккельса),характеризуется тем, что показатель преломления кристалла зависит от внешнего электрического поля.

В однородном и изотропном кристалле распространение света во все стороны равноправно и индикатриса имеет вид сферы:

,

где n ₀ – коэффициент преломления материала.

При подаче продольного напряжения U на кристалл толщиной L вдоль оси z (см. рис.4.1), получим поле с напряженностью: .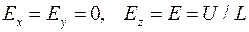

Под воздействием электрического поля вдоль оси z в кристалле меняется показатель преломления, и оптическая индикатриса приобретает следующий вид:

, (4.1)

где r ₆₃ - компонента тензора упругости.

Структурная схема испытательного стенда с электрооптическим модулятором в приведена на рис.4.1. На рисунке приняты следующие обозначения: 1- источник излучения, 2 и 7 – линзы, 3 и 6 – поляризаторы, 5 - электрооптический кристалл с прозрачными электродами, 8 - фотоприемник.

Стенд работает следующим образом. Свет от источника 1 коллимируется линзой 2 и параллельный пучок подают на модулятор, состоящий из поляризатора 3, кристалла с прозрачными электродами 5 и поляризатора-анализатора 6. Далее выходящий пучок света фокусируют на окно фотодиода 8. Под действием напряжения U(t) в кристалле создается анизотропия и поворот плоскости поляризации, приводящей к изменению амплитуды на выходе поляризатора-анализатора 6 и интенсивности тока на выходе фотодиода 8.

Таким образом, при приложении поля, одноосный кристалл превращается в двуосный, а индикатриса из круговой превращается в эллипс с разными показателями преломления для поляризационных компонент по осям y и x (n_y и n_x):

.

Фазовую и поляризационную модуляцию можно получить за счет изменения скоростей распространения поляризационных компонент по х и y:

(4.2)

Рис. 4.1. Структурная схема испытательного стенда с продольным электрооптическим модулятором (а) и ориентация осей в кристалле (б)

где Е - напряженность электрического поля.

При этом возникает двулучепреломление (ДЛП):

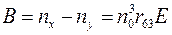. (4.3)

Фазовая задержка поляризационных компонент по оси x и по оси y:

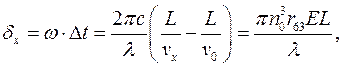
(4.4)

Разность фаз поляризационных компонент на выходе кристалла составит:

. (4.5)

Таким образом, на выходе изменяется состояние поляризации как в анизотропной среде.

Полуволновое напряжение для кристалла, соответствующее набегу фазы 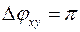будет:

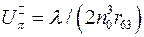. (4.6)

Для в кристалле гидрофосфата калия (КДП) - (KH₂PO₄) .

Для кристалла дигидрофосфата калия (ДКДП) - (NH₄H₂PO₄): . Для Sr_0,75Ba_0,25Nb₂O₆: .

Поперечный линейный электрооптический эффект Поккельса также наблюдается в кристаллах с кубической решеткой. Наиболее сильно он заметен в кристаллах арсенида галия GaAs, сульфита цинка ZnS, силиката висмута Bi₁₂SiO₂₀ германата висмута Bi₁₂GeO₂₀.

Рис. 4.2. Структурная схема испытательного стенда с поперечным электрооптическим модулятором (а) и ориентация осей в кристалле (б)

При воздействии электрического поля на электрооптический кристалл перпендикулярно лучу изменяются показатели преломления света в направлении y:

(4.7)

где n₀ – обыкновенный луч, n_e – необыкновенный луч.

При этом скорости распространения вертикальной и горизонтальной компонент будут определяться соотношениями:

(4.8)

ДЛП кристалла составит:

.

Разность фаз поляризационных компонент на выходе кристалла (набег фазы) составит

или , (4.9)

где d - расстояние между пластинами под напряжением U, L –длина пути в кристалле.

Исходя из (4.9) можно получить выражение для полуволнового напряжения, когда :

. (4.10)

Фазовую и поляризационную модуляцию можно реализовать, используя линейный электрооптический эффект в следующих кристаллах с кубической решеткой: GaAs – арсенид галия, ZnS – сульфит цинка, Bi₁₂SiO₂₀ – силикат висмута, Bi₁₂GeO₂₀ – германат висмута. С помощью этих веществ выполняют датчики напряжения. В этом случае компоненты тензора упругости имеют значения

,

а индикатриса имеет вид сферы

.

Продольный электрооптический эффект Поккельса. При подаче продольного напряжения на кристалл, получим поле с напряжением: . Уравнение индикатрисы приобретает следующий вид:

.

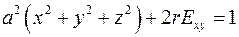Коэффициенты преломления изменяются следующим образом

(4.11)

При продольном электрическом поле разность фаз поляризационных компонент на выходе кристалла (набег фазы), как и в кристалле КДП, составит:

, (4.12)

При поперечном поле набег фаз будет:

. (4.13)

Сдвиг фаз отсутствует за счет естественной анизотропии.

Квадратичный электрооптический эффект Керра. Кристаллы, имеющие центры симметрии, и аморфные вещества обладают квадратичным эффектом (эффект Керра). Наиболее ярко квадратичный электрооптический эффект (ЭО) наблюдается у кубических кристаллов перовскитов ABO₃: BaTiO₃, KTaO₃, SrTiO₃, KTa_xNb_1-xO₃ (KTN). Этот эффект имеется также в следующих жидкостях: сероводород, нитробензол.

Уравнение индикатрисы в общем случае имеет вид:

, (4.14)

где i, j, k – индексы излучения принимают значения от 1 до 3,

слагаемое описывает линейный ЭО эффект, а – квадратичный ЭО эффект. Обычно

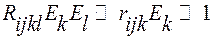. ……… (4.15)

Коэффициенты преломления меняются следующим образом для перовскитов, если :

(4.16)

где p - вектор поляризации, g₁₁, g₁₂ компоненты тензора поляризации.

Набег фаз между компонентами выражается так:

, (4.17)

где L длина.

Согласно (4.16) разность фаз пропорциональна квадрату вектора поляризации, т.е. , и отношение интенсивности света на выходе модулятора изменяется по закону:

, (4.18)

где - полуволновое напряжение.

Квадратичный эффект позволяет увеличить глубину модуляции за счет напряжения смещения U _см:

, (4.19)

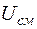где - рабочее напряжение, и - напряжения модуляции и смещения.

Незначительные изменения приводят к значительному увеличению анизотропии кристалла, высокой эффективности модуляции и к повышению быстродействия.

Поперечное полуволновое напряжение можно рассчитать по формуле:

. (4.20)

Эффективность модуляции наибольшая при U_см > 500 В.

Эффект Керра зависит и от других параметров. Например, диэлектрическая проницаемость перовскитов сильно зависит от температуры, особенно у точки Кюри .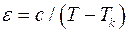

Наиболее сильный эффект Керра у KTN при .

При U _см = 300 В ().

Сероуглерод CS, нитробензол C₆H₅NO₂ и аморфин, при подаче напряжения приобретают свойства одноосных кристаллов.

Набег фазы определяется по формуле:

, (4.21)

где B_k - постоянная Керра.

Для нитробензола набег фазы в 100 раз больше, чем у другой жидкости. Свойства нитробензола: он прозрачен в области от 0,4 до 1,1 мкм, а диэлектрическая проницаемость ε велика.

Дата добавления: 2015-07-11