Распространение света

Свет в однородной среде из точки А в точку В распространяется строго прямолинейно как показано на рис. 1.6, а. Если среда не однородна, и показатель преломления меняется вдоль направления луча, например, показатель преломления зависит от координаты y – (n(y)– относительный показатель преломления), то свет распространяется по криволинейной траектории (рис.2.1, б). Это объясняется изменением скорости распространения по закону V=c/n(y) и тем, что в этом случае время распространения света между точками А΄ и В΄ должно быть минимальным.

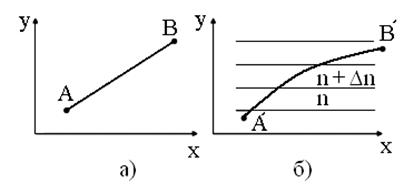
Рис. 2.1. Распространение света в различных средах: (а) - в однородной среде, (б) - в неоднородной среде, Δ n - изменение показателя преломления

В общем случае распространение световых волн подчиняется волновому уравнению:

, (2.1)

где E ₀ - напряженность электрического поля, k=2pn/l - волновое число.

Уравнение распространения луча в каждой точке имеет вид:

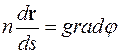, (2.2)

где r – радиус-вектор луча, s - элемент длины луча, φ – фаза волны.

Траектория луча света при прохождении в неоднородной среде n(r) из точки Р ₁ в точку Р ₂ показана на рис. 2.2. Оптическая длина пути будет следующей:

. (2.3)

В однородной среде, например, в вакууме и, следовательно,

. (2.4)

Последнее соотношение означает, что свет в однородной среде распространяется прямолинейно, и расстояние между точками будет D=cT, где Т - время распространения.

Рис. 2.2. Траектория оптического луча в неоднородной среде;

- фазовый фронт и его изменение, Р₁ и Р₂ начальная и конечная точки луча

2.2. Преломление и отражение света на границе двух
однородных сред

Законы отражения и преломления света на границе двух однородных сред были впервые сформулированы Снеллиусом:

1 - угол падения равен углу отражения: .

2 - угол падения q₁ и угол преломления q₂ на границе двух сред с коэффициентами преломления n ₁ и n ₂ связаны соотношением n ₁ sin q₁ = n ₂ sin q₂ .

На рис.2.3 показаны падающий, отраженный и преломленный лучи, а также углы по отношению к вертикальной оси, на границе двух сред с коэффициентами преломления n ₁ и n ₂.

Закон преломления Снеллиуса можно переписать в следующем виде:

, (2.5)

где V ₁= с / n ₁ и V ₂= с / n ₂ - скорости распространения света в средах с

Рис. 2.3. Схема преломления и отражения лучей на

границе двух сред

коэффициентами преломления n ₁ и n ₂.

При получим:

(2.6)

или

Это условие выполняется при .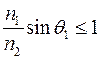

Закон преломления Снеллиуса выполняется и при обратном распространении света из среды с более высоким показателем преломления n ₂. При этом, если q₁=90º, то наблюдается полное внутреннее отражения от границы раздела верхней и нижней сред (рис.2.3).

Условие полного внутреннего отражения от границы раздела q₁=90º (sinq₁=1), имеет следующий вид:

q₂ = arcsin(n ₁/ n ₂₎. (2.7)

Условие полного внутреннего отражения от поверхности раздела сред с разными показателями преломления показывает, что свет будет удерживаться в среде с показателем преломления n ₂ при n ₂ > n ₁.

Связь плотности ρ с показателем преломления n определяется эмпирическим законом: , где - коэффициент с размерностью плотности. Чем выше плотность, тем выше n: .

Одним из важных параметров является угол Брюстера. Если отраженный и преломленный углы взаимно перпендикулярны, то отраженный луч будет линейно поляризованным. Это условие будет выполняться при , где угол

q_Б=arctg(n₂/n₁₎.

называется углом Брюстера. Пластины, расположенные под углом Брюстера, применяют для получения линейно поляризованного излучения и используют в лазерах для получения одночастотного излучения.

Дата добавления: 2015-07-11