Решения типовых примеров

Пример 1 (Вариант 6). Определить истинно или ложно высказывание «Для существования действительного логарифма числа необходимо и достаточно, чтобы это число было действительным и положительным».

Решение. Обозначим через 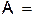«Существует действительный логарифм числа », «Число действительное и положительное». Тогда высказывание логически записывается в виде , где 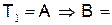«Если сущест -вует действительный логарифм числа , то – действительное и положительное», =«Если число действительное и положительное, то существует действительный логарифм ».

Высказывание , т.к. из существования следует необходимым образом, что – действительное и положительное. Следовательно, условие «Число действительное и положительное» является необходимым для условия 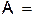«Существует действительный логарифм числа »

Высказывание , так как недостаточно чтобы было действительным и положительным для существования действительного логарифма ; ещё надо требовать , .

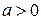По определению конъюнкции ложное высказывание .

Ответ: ложно.

Пример 2. «Для того чтобы число a являлось делителем числа 15, …, чтобы число a являлось делителем числа 5».

Решение. Введем обозначения

A (a) =«Число a – делитель числа 5»;

B (a) =«Число а – делитель числа 15».

Для проверки необходимости (!) условия A (a) для условия B (a) выясним, истинна ли теорема T = B (a) A (a), т.е. Т =«Если число а – делитель числа 15, то а – делитель числа 5». Так как найдется такое значение а, например, а =3, при котором B (a)=И, а A (a)=Λ, т.е. ложно высказывание T = B (a) A (a) и, следовательно, A (a) не является необходимым условием для B (a).

Для проверки достаточности условия A (a) для условия B (a) выясним, находятся ли A (a) и B (a) в отношении следования, т.е. истинна ли теорема T = A (a) B (a)=«Если число а – делитель числа 5, то а – делитель числа 15». Так как любой делитель числа 5 (т.е. 1 и 5) является и делителем числа 15, то =И. Следовательно, условие А (а) является достаточным условием для В (а).

Таким образом, вместо многоточия нужно вставить выражение «достаточно, но не необходимо».

Ответ: достаточно, но не необходимо.

Дата добавления: 2015-10-21