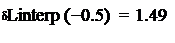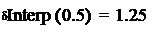Интерполирование с помощью системы Mathcad
1. Запишем исходные данные для расчёта:
2. Построим график для визуализации исходных данных:
 Рисунок 1. Кусочно-линейная графическая интерполяция исходных данных средствами Mathcad.
Рисунок 1. Кусочно-линейная графическая интерполяция исходных данных средствами Mathcad.
|
3. Напишем подпрограмму для определения промежуточных точек по формуле Лагранжа:
4. Запишем имеющиеся данные при помощи двух пар векторов. Векторы z1 и f1 соответствуют исходным данным, а векторы z и f полному набору точек с учетом полученных промежуточных значений:
5. Представим записанные векторы в графическом виде с использованием автоматической кусочно-линейной интерполяции Маthcad:
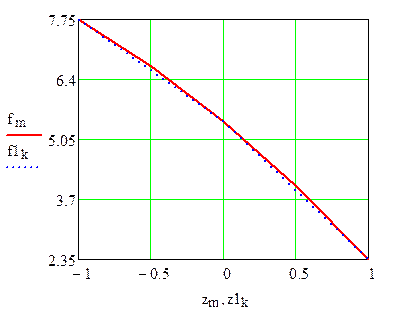 Рисунок 2. Кусочно-линейная графическая интерполяция данных: f1k - исходные, fm - дополненные расчетом по формуле Лагранжа.
Рисунок 2. Кусочно-линейная графическая интерполяция данных: f1k - исходные, fm - дополненные расчетом по формуле Лагранжа.
|
6. После подстановки исходного вектора данных:
интерполяционный полином примет следующий вид:


Полученные результаты соответствуют результатам подпрограммы.
7. Воспользуемся операторами linterp (кусочно-линейчатая интерполяция) и interp (интерполирование кубическим сплайном):
 Рисунок 3. Интерполяция данных обычным полиномом Lagr(zx), сплайн-интерполяцией Intrp(zx), кусочно-линейной функцией Linterp(zx).
Рисунок 3. Интерполяция данных обычным полиномом Lagr(zx), сплайн-интерполяцией Intrp(zx), кусочно-линейной функцией Linterp(zx).
|
Вывод
Пользуясь различными методами интерполяции, мы получили три разных набора данных, представленных в таблице 2.
Таблица 2
| x
| y
|
| Lagrang
| Linterp
| Interp
|
| -1
| 7.75
| 7.75
| 7.75
|
| -0.5
| 6.7
| 6.60
| 3.90
|
|
| 5.45
| 5.45
| 5.45
|
| 0.5
|
| 6.75
| 3.95
|
|
| 2.35
| 2.35
| 2.35
|
Рассчитаем абсолютную и относительную погрешности относительно значений, которые мы получили по формуле Лагранжа при  и при
и при 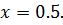 Погрешность в узлах интерполирования равна нулю.
Погрешность в узлах интерполирования равна нулю.
Формулы для расчёта абсолютной погрешности:
Формулы для расчёта относительной погрешности:
Расчёт погрешностей:
Погрешность расчётов оказалась достаточно мала (до 3%). Можно сказать, что интерполирование произведено с высокой точностью
Дата добавления: 2015-10-21; просмотров: 128 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.008 сек.)

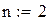
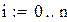


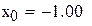





 Рисунок 1. Кусочно-линейная графическая интерполяция исходных данных средствами Mathcad.
Рисунок 1. Кусочно-линейная графическая интерполяция исходных данных средствами Mathcad.



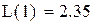

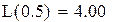






 Рисунок 2. Кусочно-линейная графическая интерполяция данных: f1k - исходные, fm - дополненные расчетом по формуле Лагранжа.
Рисунок 2. Кусочно-линейная графическая интерполяция данных: f1k - исходные, fm - дополненные расчетом по формуле Лагранжа.
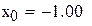







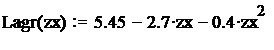








 Рисунок 3. Интерполяция данных обычным полиномом Lagr(zx), сплайн-интерполяцией Intrp(zx), кусочно-линейной функцией Linterp(zx).
Рисунок 3. Интерполяция данных обычным полиномом Lagr(zx), сплайн-интерполяцией Intrp(zx), кусочно-линейной функцией Linterp(zx).
 и при
и при 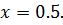 Погрешность в узлах интерполирования равна нулю.
Погрешность в узлах интерполирования равна нулю.