Теоретические сведения. В промежутке [-1;1] по оси задано (табл

Задание

В промежутке [-1;1] по оси задано (табл. 1) три значения аргумента и соответствующие им значения дискретной функции .

Таблица 1

-1.0	7.75
-0.5	-
	5.45
0.5	-
	2.35

По исходным данным в таблице 1 нужно определить при двух промежуточных значениях и 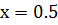c точностью до двух знаков после запятой.

Теоретические сведения

Интерполяция обычными полиномами обеспечивает непрерывность производных во всех узлах кроме граничных, и заключается в нахождении полинома низшей степени, принимающего заданное значение в исходных точках. Обычный полином

в узлах интерполяции x₀,x₁,...x_n должен точно совпадать со значениями функции y₀,y₁,...y_n. Как известно, существует единственный полином степени не выше n, принимающий в точках x₀,x₁...x_n заданные значения. Поэтому m=n, при этом число узлов интерполирования на единицу больше, чем степень полинома. Степень полинома равна числу интервалов, на которые разделяется весь промежуток интерполирования. Коэффициенты a_i полинома Q_n(x) можно определить различными способами.

1.Из решения системы уравнений

Порядок системы равен числу узлов интерполирования, т.е. n+1. Решение системы может быть получено способом Крамера с помощью определителей или способом Гаусса путем исключения переменных.

Подставим в систему исходные данные:

Последовательным исключением переменных получим

При этом интерполирующий полином примет вид

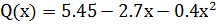
2. По формуле Лагранжа, позволяющей определить полином при произвольных узлах интерполяции.

Подставим исходные данные в формулу Лагранжа:

.

Как видно, по формуле Лагранжа мы получили тот же результат, что и в предыдущем способе.

3. По формуле Ньютона, позволяющей определить полином при равноотстоящих с шагом в узлах интерполирования.

где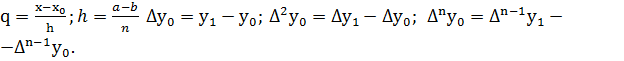

При определении значений функции f(x) в точке x по формулам Лагранжа или Ньютона в качестве начальной точки выгодно брать ближайший к x узел интерполирования. Тогда первое слагаемое в этой формуле будет главным членом, а остальные слагаемые будут носить характер поправки.

Подставим в формулу Ньютона исходные данные:

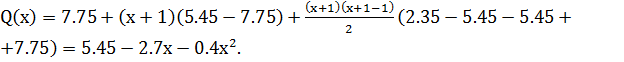
Разными способами мы получили одно и то же выражение для интерполяционного полинома, проходящего через три заданные точки.

Дата добавления: 2015-10-21