Этапы формирования портфеля

В данной курсовой работе для нахождения инвестиционного портфеля для компаний Сургутнефтегаз, Юкос, Сибнефть, РАО «ЕЭС России» была выбрана модель Марковица, которая успешно реализуется в Microsoft Office Excel 2007.

Основная идея модели Марковица заключается в том, чтобы статистически рассматривать будущий доход, приносимый финансовым инструментом, как случайную переменную, т.е. доходы по отдельным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом определить по каждому инвестиционному объекту вполне определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств.

По модели Марковица определяются показатели, характеризующие объем инвестиций и риск, что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.

В качестве, масштаба ожидаемого дохода из ряда возможных доходов на, практике используют наиболее вероятное, значение, которое в случае нормального распределения совпадает с математическим ожиданием.

Для измерения риска служат показатели рассеивания, поэтому, чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Таким образом, риск выражается отклонением (причем более низких!) значений доходов от наиболее вероятного значения. Мерой рассеяния является среднеквадратичное отклонение и, чем больше это значение, тем больше риск.

При помощи разработанного Марковицем метода критических линий можно выделить неперспективные портфели, не удовлетворяющие ограничениям. Тем самым остаются только эффективные портфели, т.е. портфели, содержащие минимальный риск при заданном доходе или приносящие максимально возможный доход при заданном максимальном уровне риска, на который может пойти инвестор[3].

Данный факт имеет очень большое значение в современной теории портфелей ценных бумаг. Отобранные таким образом портфели объединяют в список, содержащий сведения о процентном составе портфеля из отдельных цепных бумаг, а также о доходе и риске портфелей. Выбор конкретного портфеля зависит от максимального риска, на который готов пойти инвестор.

С методологической точки зрения модель Марковица можно определить как практически-нормативную, что, конечно, не означает навязывания инвестору определенного стиля поведения на рынке ценных бумаг. Задача модели заключается в том, чтобы показать, как поставленные цели достижимы на практике[2, 5].

1.Исходные данные

Исходными данными являются сведения о рыночной стоимости обыкновенных акций на начало месяца для сегмента фондового рынка, состоящего из 4 компаний, указанные в таблице, подготовленной в среде Excel.

Рис.1: Таблица «Исходные данные»

2. Определение доходности активов рассматриваемых компаний

Доходность – важнейшая количественная характеристика инвестиционного актива, тесно связанная с данным промежутком времени; одна из важнейших целей инвестора. Полный доход инвестора за определенный период времени складывается не только из прироста стоимости инвестиционного капитала (капитального дохода), но и из так называемого текущего дохода, который он получает в виде дивидендов, процентов, платежей, получаемых от сдачи в аренду недвижимости и др[3]. Таким образом

Полный доход = Текущий доход + Прирост капитала.

Количественной характеристикой способности актива приносить прибыль является ее доходность для заданного периода Т:

где Div_T – текущий доход, полученный от актива а в течение данного периода;

P₀ – стоимость (цена) актива в начале периода;

P₁ – стоимость (цена) актива в конце периода.

Для расчета доходностей активов необходимо ввести формулы в соответствующие ячейки. Программа Excel рассматривает содержимое ячейки как формулу, если оно начинается со знака равенства (=). Тем самым, чтобы начать ввод формулы в ячейку, достаточно нажать клавишу «=». Например, для того чтобы определить доходность акции компании «Сургутнефтегаза» в первом периоде достаточно выделить ячейку D34 и набрать в ячейке формулу =(C5-C4)/C4 (значение в ячейке С4 – стоимость актива в конце 1 периода, С5 – стоимость актива в конце 2 периода) следующим образом: сначала введем знак равенства, затем введем символ “(“, переместим указатель теперь в клетку С5, введем “-” и т.д. После ввода всей формулы нажмем клавишу [Enter] и в ячейке D36 получим результат.

Рис.2: Расчет доходности

Как видно из полученной таблицы доходностей, доходности акций могут быть и отрицательными, если стоимость актива не растет, а падает.

3. Построение графики изменения месячной доходности акций компаний

Для наиболее наглядного представления полученные результаты можно отразить на графике, используя средства Excel.

Установите курсор на ячейку, где хотите расположить график и вверху в меню переключитесь на вкладку «Вставка». Затем нажмите на кнопку «График», выпадет несколько их видов. Выбрать можно любой, какой больше нравится, на сложность построения это не повлияет, только на внешний вид. На листе Excel появится новый объект - чистый график. Когда он выделен, то верхняя панель с иконками действий имеет другой вид, специально для работы с графиками. Чтобы заполнить график, нажмите на кнопку «Выбрать данные». Отобразится окно выбора данных для графика. В нем имеется поле «Выбор данных для диаграммы». В конце поля необходимо нажать на кнопку выбора диапазона. Окно выбора данных пример сокращенный вид. Вам следует выделить мышкой на листе Excel таблицу с данными доходностями и выбрать с $C$33 по $G$58 Окно выбора данных развернется до полного вида, и Вы увидите, что поле «Выбор данных для диаграммы» наполнено данными. Нажмите «ОК». В результате будет построен график с несколькими линиями. Они отличаются цветом[6].

Рис.3: График доходностей

По графику видно, что наибольшие колебания курсовой стоимости наблюдаются у акций компании РАО “ЕЭС России”: они обладали наибольшей доходностью за период аперель-май 2003 г. и соответственно наименьшей доходностью – май-июнь 2002 г.

4. Оценка ожидаемой доходности и риска акций, построение ковариационной матрицы, используя данные по февраль 2004 г.

Доходность, вы­численная по ожидаемым значениям текущего дохода и будущей стои­мости, называется ожидаемой доходностью. Именно она является важней­шим ориентиром в принятии решения при инвестировании. Инвестор стремится вложить средства в наиболее доходные активы. Естественно, на практике реальные значения этих величин могут отличаться от ожидаемых. Степень отличия и представляет собой риск инвестирования.

Ожидаемая доходность актива представляется в виде математического ожидания:

где r_k – доходность i-го актива в k-тый момент времени, k=1,N.

В среде Microsoft Office Excel подготовим таблицу ожидаемых доходностей активов. Для первого актива формула определения ожидаемой доходности будет иметь вид: =(1/25)*СУММ(D34:D58).

Рис.4: Таблица «Ожидаемые доходности»

По полученным результатам видно, что наибольшей доходностью обладают акции компаний Сибнефть и РАО «ЕЭС России».

Следующей важнейшей характеристикой случайных величин является дисперсия, которая характеризует «степень отклонения» (разброс) случайной велечины – ожидаемой доходности.

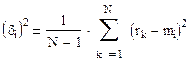
Из определения дисперсии видно, что она имеет размерность квадрата размерности случайной величины. Для того чтобы использовать в качестве меры разброса характеристику той же размерности, вместо дисперсии часто используют среднеквадратичное или стандартное отклонение:

Найдем дисперсию и стандартное отклонение для доходностей приведенной модели по выше приведенным формулам, предварительно центрировав доходности активов рассматриваемых компаний. Например, формула для определения центрированной доходности первого актива в первом периоде будет иметь вид: =D34-B$92.

Рис.5: Центрированные доходности

Найдем дисперсии и стандартные отклонения, воспользовавшись встроенными функциями:

Рис.6: Нахождение дисперсии и СКО

Выбор двух количественных характеристик, или критериев – ожидаемой доходности и риска, делает задачу выбора оптимальной стратегии инвестирования двухкритериальной. Если эта стратегия состоит в инвестировании всего капитала лишь в актив одного вида, то необходимо, чтобы он был наилучшим сразу по двум критериям, т.е. обладал наибольшей доходностью и наименьшим риском[4].

На практике такое встречается достаточно редко, поэтому инвестор вынужден вместо выбора одного актива составить портфель из них, стремясь по возможности «диверсифицировать» (перераспределить) риск с целью уменьшения его количественной оценки. Это перераспределение рисков связано с ковариацией активов, которая является мерой взаимодействия двух случайных величин:

Составим ковариационную матрицу для акций 9 исследуемых компаний. Для этого воспользуемся встроенной функцией КОВАР, которая используется для определения связи между двумя массивами данных. Так, для нахождения ковариации между активами компаний «Сургутнефтегаз» и «Юкос» воспользуемся формулой =(КОВАР($D$34:$D$58;E34:E58)*25)/24.

Аналогично определяются остальные элементы ковариационной матрицы.

Рис.7: Ковариационные матрицы

Таким образом, ковариация - есть это мера того, насколько две случайные переменные, такие, например, как доходности двух ценных бумаг, зависят друг от друга.

Положительное значение ковариации показывает, что доходности этих ценных бумаг имеют тенденцию изме­няться в одну сторону, например лучшая, чем ожидаемая, доходность одной из ценных бумаг должна, вероятно, повлечь за собой лучшую, чем ожидаемая, доходность другой ценной бумаги (Например, ковариация между акциями компаний «Сибнефть» и «Юкос» составляет 0,008388968).

Отрицательная ковариация показывает, что доходности имеют тенден­цию компенсировать друг друга, например лучшая, чем ожидаемая, доходность одной ценной бумаги сопровождается, как правило, худшей, чем ожидаемая, доходностью другой ценной бумаги.

Относительно небольшое или нулевое значение ковариации показывает, что связь между доходностью этих ценных бумаг слаба либо отсутствует вообще, как например, у компаний «Сургутнефтегаз» и «Сибнефть» (0,00190065).

Отметим некоторые интересные свойства ковариационной матрицы. Во-первых, матрица является квадратной, т.е. количество столбцов равняется количеству строк, в нашем случае полученная матрица имеет размерность 4x4.

Во-вторых, дисперсии ценных бумаг лежат на диагонали матрицы, которая пред­ставляет собой ячейки, лежащие на линии, проходящей из левого верхнего угла матрицы в правый нижний угол.

В-третьих, матрица, является симметричной. Это означает, что элемент, располо­женный в i-ой строке j-ого столбца равен элементу, расположенному в j-ой строке i-ого столбца. То есть элементы ячеек, расположенных над диагональю, повторяются в соот­ветствующих ячейках, расположенных под диагональю, т.е. ковариация между двумя ценными бумагами не зависит от порядка, в котором эти две бу­маги упоминаются. Это означает, что, например, ковариация между ценными бумагами «Сургутнефтегаз» и «Сибнефть» является такой же, как и ковариация между «Сибнефть» и «Сургутнефтегаз»[1, 4].

5. Определение состава активов, включаемых в портфель Марковица, используя метод главного критерия; составление портфеля при различных рисках, используя функцию полезности; построение линию эффективных портфелей допустимого множества

Важнейшим этапом инвестиционного процесса является формирование портфеля ценных бумаг, т.е. определение конкретных активов для вложения средств, а также пропорций распределения инвестируемого капитала между активами.

Наличие двух критериев значительно осложняет выбор оптимального портфеля, поскольку, улучшая значение одного критерия, как правило, ухудшается значение другого. Имеется несколько подходов к решению задачи выбора портфеля с наличием нескольких критериев. Первый подход основан на выборе главного критерия, по которому будет осуществляться оптимизация. Считая главным критерием риск, рассматривая доходность в качестве критериального ограничения, сформулируем задачу квадратичного программирования, которая позволит выбрать оптимальный портфель с минимальным риском и доходностью не ниже наперед заданного значения[1, 2]:

Определим диапазон изменения допустимых доходностей портфеля, используя встроенные функции МАКС и МИН пакета Excel:

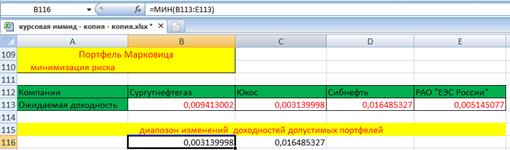
Рис.8: Портфель Марковица – минимизация риска

В среде Microsoft Office Excel мощным и достаточно эффективным инструментом решения оптимизационных задач является программная надстройка Поиск решения, которая входит в поставку программного продукта и может устанавливаться по желанию пользователя.. На выбранном рабочем листе зададим ячейки, которые будут предназначены для сохранения переменных решаемой задачи х1, х2, …, хn: переменная х1 содержится в ячейке Е122, х2 – Е125 и т.д. (обычно для хранения имен переменных используют смежные ячейки), присвоив им любые начальные значения, удовлетворяющие ограничениям xi≥0 и

Перед тем, как сформулировать решающую функцию, произведем вспомогательные вычисления для определения величины риска при заданных начальных условиях:

• Транспонируем вектор-столбец x, который содержится в диапазоне ячеек Е122:Е125, используя встроенную функцию ТРАНСП, которая должна быть введена как в интервал, имеющий столько же строк и столбцов, сколько столбцов и строк имеет исходный массив – А120:D120. В ячейке А120 выражение будет иметь вид: =ТРАНСП(Е122:Е125).

Формулу необходимо ввести как формулу массива, т.е. после копирования необходимо выделить диапазон Е122:Е125, начиная с ячейки Е122, содержащей формулу, нажать клавишу F2 и сочетание клавиш CTRL+SHIFT+ENTER.

Рис.9: Транспонирование вектора-столбца х

Найдем значение произведения двух массивов данных - вектора-строки xt и ковариационной матрицы С – путем использования встроенной функции МУМНОЖ, которая является функцией массива:

=МУМНОЖ(A120:D120;B103:E106).

• На последнем шаге вычисляем величину риска, значение которой занесем в клетку A130, по формуле: =МУМНОЖ(А112:D112;E122:E125).

Рис.10: Нахождение целевой функции

Зададим ячейку, содержащую формулу целевой функции решаемой задачи. В нашем примере значение целевой функции есть величина риска, которая была предварительно вычислена, поэтому ячейка А133 будет содержать ссылку на ячейку А133: =А130. Заполнение ячеек критериальными ограничениями. Для этого используются клетки:

А135– для ввода ограничения на доходность

=МУМНОЖ(B92:E92;E122:E125);

А136– доля всех активов в портфеле должна быть равна 1 =СУММ(E122:E125)

Рис.11: Ограничения

В Поиске решения задаём тип оптимизации, адрес целевой ячейки,адреса ячеек данных, систему ограничений[6].

Рис.12: Поиск решений

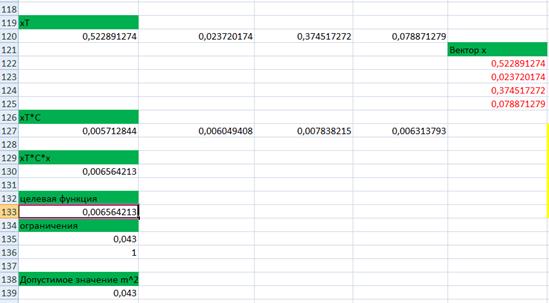
Рис.13: Допустимые значения

Применение надстройки Поиск решения позволило нам определить при заданной доходности эффективный портфель, составленный из 4 компаний исследуемого сегмента фондового рынка. По полученным результатам видно, что осторожному инвестору на рынке рискованно приобретать акции компании Юкос.

Эффективным множеством или эффективной границей называется набор портфелей, удовлетворяющих этим двум условиям:

1. Обеспечивает максимальную ожидаемую доходность для некоторого заданного уровня риска;

2. Обеспечивает минимальный риск, удовлетворяющий некоторому заданному инвестором уровню доходности.

Для построения эффективной границы будем использовать 6 точек. Определим величину шага по формуле: =(C116-B116)/5.

Таким образом, варьируя возможные значения доходности портфеля из диапазона [m_min, m_max] и находя соответствующие решения задачи оптимизации, построим эффективную границу допустимого множества, которая лежит правее оценки портфеля с наименьшим риском.

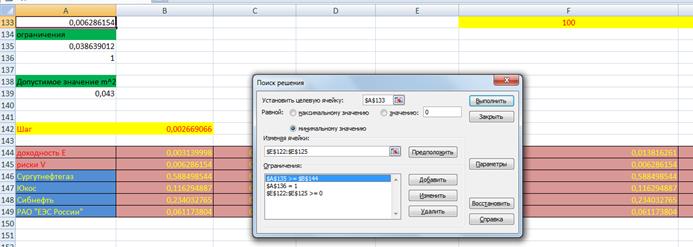Построим таблицу, где будет изменятся при заданной доходности риск и акции компаний.

Рис.14: Таблица изменений доходности и риска

При построении диаграммы- «эффективной границы» в качестве исходных данных выберем диапазон ячеек: С144:G145, который будут на ней отображаться.

Рис.15: Диаграмма – Эффективная граница

По полученным результатам, видно, что риск оптимального портфеля не возрастает вместе с ростом ожидаемой доходности.. Максимальной доходностью обладает портфель, образованный из активов с максимальной ожидаемой доходностью. В нашем примере это последний оптимальный портфель, составленный из акций 3 крупных компаний: Сургутнефтегаз, Сибнефть, РАО «ЕЭС России».

6. Оценка полной доходности портфеля за март 2004 года

Для этого вычисляется доход портфеля по формуле

где 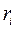- доходность акции - й компании за март месяц 2004 года.

Рис.16: Доходность за март 2004 г.

Из выше приведенного рисунка видно, что наибольший доход за март 2004 года имеет компания «Сургутнефтегаз», а наименьший «РАО «ЕЭС России»», поэтому инвестору выгоднее вложить свой капитал в «Сургутнефтегаз».

Заключение

Практика показывает, что портфельным инвестированием сегодня интересуются два типа клиентов. К первому относятся те, перед кем остро стоит проблема размещения временно свободных средств (крупные и инертные государственные корпорации, выросшие из бывших министерств, различные фонды, создаваемые при министерствах, и другие подобные структуры, а также клиенты из тех регионов, где рынок не способен освоить крупные средства). Ко второму типу относятся те, кто, уловив эту потребность "денежных мешков" и остро нуждаясь в оборотных средствах, выдвигают идею портфеля в качестве "приманки" (не очень крупные банки, финансовые компании и небольшие брокерские конторы).

Конечно, многие клиенты не до конца отдают себе отчет, что такое портфель активов, и в процессе общения с ними часто выясняется, что на данном этапе они нуждаются в более простых формах сотрудничества. Да и уровень развития рынков в различных регионах разный - во многих регионах процесс формирования класса профессиональных участников рынка и квалифицированных инвесторов еще далеко не завершен. Тем не менее, усиление клиентского спроса на услуги по формированию инвестиционного портфеля в последнее время очевидно. Это говорит о том, что вопрос назрел.

На основе полученных данных о доходности акций мы можем сделать вывод о компаниях на будущий период времени, куда следует вкладывать деньги, а куда нет. Из наших 4 компаний, инвестору опаснее всего будет вкладывать свой капитал в акции компании «Юкоса»[5].

Список используемой литературы

1. Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. М.: Филинъ, 1998. 144 с.

2. Шведов А.С. Теория эффективных портфелей ценных бумаг. М.: ГУВШЭ, 1999. 144 с.

3. Шарп У.Ф. и др. Инвестиции. М.: Высшая школа, 1993. 668 с.

4. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. М.: Высшая школа, 1989. 367 с.

5. http://works.tarefer.ru/28/100127/index.html

6. http://www.infowall.ru/index.php?menu_id=openprogarticle&art_id=465

Дата добавления: 2015-10-21