Резонансные частоты свободных колебаний

В рассматриваемом случае уравнения Максвелла (1.33) и (1.39) можно переписать в виде

Слева в (11.6) стоит квадрат резонансной угловой частоты объемного резонатора, а справа - всегда положительная вели­чина, равная отношению двух объемных интегралов. Численное значение каждого из этих интегралов зависит от формы объема Vo и его размеров, а также от характера подынтегральной функции. Поэтому резонансная частота резонатора зависит от структуры попей в резонаторе, его формы и размеров.

Структура полей в резонаторе, как и в направляющих сис­темах, определяется путем решения уравнений Максвелла при определенных граничных условиях на поверхности, окружающей объем V_o. В случае закрытых резонаторов без потерь задача сво­дится к решению трехмерного векторного волнового уравнения:

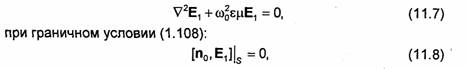
где S - внутренняя поверхность металлической оболочки резона­тора, а n₀ - орт нормали к этой поверхности.

Можно доказать, что уравнение (11.7) при граничном условии (11.8), как и аналогичные уравнения теории направляющих систем, имеет бесконечное число различных решений, каждому из которых согласно (11.6) соответствует определенное значение резонан­сной угловой частоты ω₀, т.е. объемные резонаторы, в отличие от обычных контуров из сосредоточенных элементов, резонируют не на одной частоте, а на бесконечном множестве дискретных частот ωo₁, ω₀₂.....ω_0p.....То колебание, которому при данных размерах резонатора соответствует минимальная резонансная частота ω_О1, называют низшим колебанием. Отметим, что каждой резонансной частоте соответствует определенная структура электромагнитного поля в резонаторе.

Не исключено, что в объемном резонаторе резонансные час­тоты двух или большего числа колебаний с различной структурой полей совпадут. Обладающие этим свойством колебания принято называть вырожденными.

Дата добавления: 2015-10-21