Торможение при переменном коэффициенте сцепления

В практике нередки случаи, когда заторможенный автомобиль последовательно перемещается по двум участ­кам дороги с различными значениями коэффициента сцепления. Например, торможение, начатое на сухом асфальтобетоне, продолжается на участке, покрытом сне­гом или коркой льда. Аналогичное явление наблюдается, когда заторможенный автомобиль выходит за пределы проезжей части и останавливается на грунтовой обочине.

Рассмотрим движение автомобиля в указанных условиях.

Пусть в процессе ДТП длина тормозного следа на участке дороги с коэффициентом сцепления составила S_ю1 , а на участке с (рис. 3.6, а). В эксперт­ной практике начальную скорость автомобиля примени­тельно к этому случаю определяют как

(3.33)

где j₁ и j₂ — замедления автомобиля на первом и втором участках.

Как показано ниже, если длины пути S_ю1 и S_ю2 имеют тот же порядок, что и база автомобиля, то формула (3.33) может привести к крупной ошибке и пользоваться ею не следует.

Весь процесс движения заторможенного автомобиля состоит из трех фаз.

Первая фаза начинается в момент блокировки колес-(положение 1 на рис. 3.6, а) и заканчивается в момент въезда передних колес на второй участок (положение 2). В первой фазе автомобиль движется с замедлением j₁, длина пути равна

Рис. 3.6 Схема к расчету замедления при торможении на участках с различными коэффициентами продольного сцепления ;

а – тормозные следы; б – силы, действующие на автомобиль; в – график замедления.

Вторая (переходная) фаза начинается в момент въезда передними колесами на второй участок и продол­жается до тех пор, пока задние колеса автомобиля не пересекут границу между участками. Замедление во второй фазе j_1-2. Перемещение автомобиля в этой фазе, очевидно, равно L.

Третья фаза заканчивается в момент остановки авто­мобиля в конце второго участка (положение 3). Замед­ление автомобиля в третьей фазе j₂, а перемещение .

Для упрощения примем, что замедление изменяется мгновенно в момент пересечения передними колесами автомобиля границы между участками дороги с различ­ными коэффициентами сцепления и сохраняется постоян­ным в течение каждой из фаз.

Согласно условиям равновесия (рис. 3.6,6):

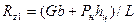
(3.34)

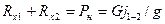(3.35)

где 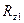и 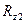— нормальные, а и — касательные реакции дороги, действующие на переднюю и заднюю оси автомоби­ля соответственно; а, b и — расстояния от центра тяжести автомобиля соответственно до его переднего и заднего мос­тов и до поверхности дороги, м.

Предполагая полное использование сцепления шинами всех колес автомобиля в переходной фазе, можно напи­сать:

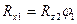(3.36)

Подставим в формулу (3.35) значения и , полу­ченные из выражений (3.36), определим значение силы инерции в промежуточной фазе движения: .

Отсюда сила

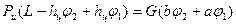
Определив из последнего выражения и учитывая формулу (3.35), получаем

(3.37)

Замедление зависит от коэффициентов сцепления на обоих участках дороги и от параметров автомобиля. Поэтому (в отличие от замедлений j₁ и j₂) замедление во второй фазе торможения различно для автомобилей разных типов. Кроме того, оно зависит от соотношения коэффициентов сцепления и (рис. 3.6, в).

Определим теперь основные параметры движения авто­мобиля.

Скорость автомобиля в начале третьей фазы . Скорость автомобиля в начале переходной (второй) фазы 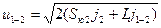. Скорость автомо­биля в начале первой фазы (в момент возникновения следа юза на дорожном покрытии) 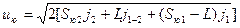. Начальная скорость автомобиля с учетом его замедления в течение t₃:

. (3.38)

Сравним-результаты расчета по выражениям (3.33) и (3.38).

При 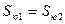= 5 м; = 0,6; = 0,2; а = b = 2 м;

t₃ = 0,2 с и = 0,7 м замедление во второй фазе равно 3,7 м/с².

Рис. 3.7. Зависимость коэф­фициента продольного сцепления от скорости движения:

— начальное значение коэф­фициента

Начальная скорость автомобиля согласно формуле (3.33) = 9,6 м/с.

Та же скорость, вычисленная по формуле (3.38).

= 8,45 м/с.

Разница между значениями 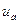, вычисленными раз­личными способами, оказалась равной 1,1 м/с, или 13%, что может оказать влияние на выводы эксперта.

Время движения автомобиля находим на основании соображений, аналогичных приведенным выше. Время движения в третьей фазе . Время дви­жения во второй фазе 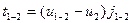. Время дви­жения в первой фазе 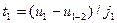. Остановочное время автомобиля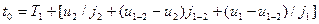

Сравнительно недавно, когда скорости автомобиля и качество тормозной системы были невысокими, экспери­ментаторы ограничивались небольшими диапазонами из­менения скорости, в которых коэффициент можно было считать постоянным. В настоящее время можно с уверенностью констатировать уменьшение коэффициента сцепления с увеличением начальной скорости автомо­биля. Один из типичных графиков показан на рис. 3.7. Уменьшение означает увеличение пути и времени торможения автомобиля, особенно в зоне высоких скоростей, и, как следствие, существенное ухуд­шение безопасности.

Учет функциональной связи между и скоростью осложняет экспертные расчеты. Поэтому при ориентиро­вочных расчетах поступают следующим образом. Задав­шись в соответствии с обстоятельствами ДТП пример­ными значениями начальной и конечной скоростей (напри­мер, u₁ и u₂), аппроксимируют соответствующий участок кривой прямой линией АВ и находят среднее значение коэффициента сцепления в данном интервале

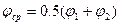
где и — значения коэффициента на границах интервала.

После этого определяют замедление и начальную скорость автомобиля. Если начальная скорость заметно отличается от предполагаемого значения u₂ , расчет по­вторяют.

Более точные результаты получают, описав прямо­линейный отрезок уравнением вида:

.

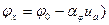где — тангенс угла наклона прямой АВ.

Тогда уравнение пути приобретает следующий вид: .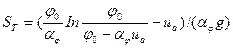

Время торможения

При аппроксимации большого участка кривой, напри­мер, уравнением гиперболы, получаем еще более сложные формулы.

При наличии ЭВМ использование этих формул не представляет особых трудностей, однако, учитывая ма­лую точность основных исходных данных, обычную в делах о ДТП, применение подобных выражений в эксперт­ной практике вряд ли целесообразно.

Дата добавления: 2015-10-16