
|
Читайте также: |
СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА
Как для некоторых функций существуют обратные функции, так и для производной существует обратная. В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения: например,
§ возведение в квадрат  и извлечение квадратного корня
и извлечение квадратного корня  ;
;
§ синус и арксинус и т.д.
Для производной функции обратная – первообразная. Процесс отыскания производной по заданной функции называют дифференцированием, а обратную операцию, т.е. процесс отыскания функции по заданной производной — интегрированием.
Определение: Функцию 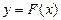 называют первообразной для функции
называют первообразной для функции 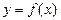 на заданном промежутке
на заданном промежутке  , если для всех
, если для всех 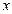 из
из  выполняется равенство
выполняется равенство 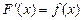 .
.
На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции.
Для того, чтобы доказать, что функция 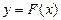 является первообразной функции является первообразной функции 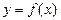 на промежутке на промежутке  , нужно показать, что для всех , нужно показать, что для всех 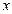 из этого промежутка выполняется равенство из этого промежутка выполняется равенство 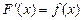 (т.е. воспользоваться определением). (т.е. воспользоваться определением).
|
Примеры:
1. Докажите, что  является первообразной для функции
является первообразной для функции 
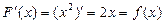
Полученное равенство верно для всех действительных значений х.
2. Докажите, что 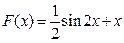 является первообразной для функции
является первообразной для функции 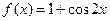 на R
на R
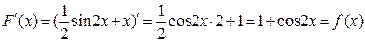
Полученное равенство верно для всех действительных значений х.
Задание 1: Докажите, что 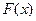 является первообразной для функции
является первообразной для функции 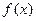

Задание 2: Докажите, что 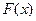 является первообразной для функции
является первообразной для функции 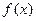
а) 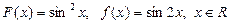 б)
б) 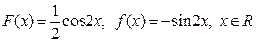
в)  г)
г) 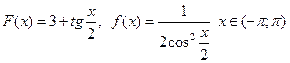
Основное свойство первообразной.
Определение 1: Если 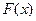 одна из первообразных функции
одна из первообразных функции 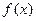 на заданном промежутке
на заданном промежутке  , то любая первообразная функции
, то любая первообразная функции 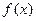 на этом промежутке имеет вид
на этом промежутке имеет вид  .
.
Определение 2: Если 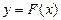 первообразная для функции
первообразная для функции 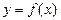 на заданном промежутке
на заданном промежутке  , то у функции
, то у функции 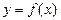 бесконечно много первообразных и все они имеют вид
бесконечно много первообразных и все они имеют вид  .
.
Таблица первообразных.

Правила нахождения первообразных.
При отыскании первообразных, как и при отыскании производных, используются не только формулы (таблица), но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.
Правило 1. Первообразная суммы равна сумме первообразных.
Правило 2. Постоянный множитель можно вынести за знак первообразной.
Правило 3: Если 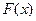 первообразная для функции
первообразная для функции 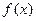 на заданном промежутке
на заданном промежутке  ,
, 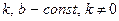 то функция
то функция 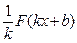 есть первообразная для функции
есть первообразная для функции 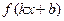
Пример. Найти первообразную функции 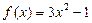 , график которой проходит через точку М(1; -1)
, график которой проходит через точку М(1; -1)
Задание 3: Найдите одну из первообразных функции
а) 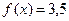 б)
б) 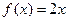
в) 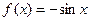 г)
г) 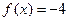
д) 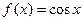 е)
е) 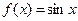
ж)  з)
з) 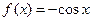
Задание 4: Найдите общий вид первообразных функции 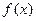
а) 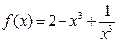 б)
б) 
в) 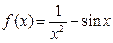 г)
г) 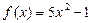
д) 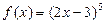 е)
е) 
ж) 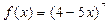 з)
з) 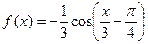
и)  к)
к) 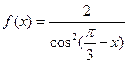
л) 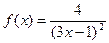 м)
м) 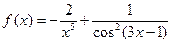
н)  о)
о) 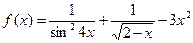
п) 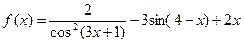 р)
р) 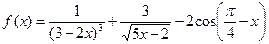
Задание 5: Найти первообразную функции 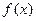 , график которой проходит через точку М
, график которой проходит через точку М
а)  б)
б) 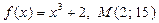
в)  г)
г) 
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
Теорема: Если 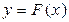 - первообразная для функции
- первообразная для функции 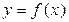 на промежутке I, то у функции
на промежутке I, то у функции 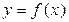 бесконечно много первообразных и все они имеют вид
бесконечно много первообразных и все они имеют вид 
Определение: Если функция 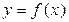 имеет на промежутке I первообразную
имеет на промежутке I первообразную 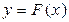 , то множество всех первообразных, т.е. множество функций вида
, то множество всех первообразных, т.е. множество функций вида  , называют неопределенным интегралом от функции
, называют неопределенным интегралом от функции 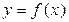 и обозначают:
и обозначают:
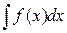
(читают: «неопределенный интеграл эф от икс дэ икс»).
Таблица интегралов.

8. 
9. 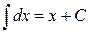
10. 
11. 
Правила интегрирования.
Правило 1. Интеграл от суммы функций равен сумме интегралов этих функций:
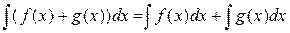
Правило 2. Постоянный множитель можно вынести за знак интеграла:
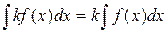
Правило 3. Если 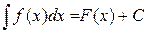 , то
, то 
Задание 6: Найти неопределенные интегралы:
а) 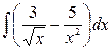 ; б)
; б) 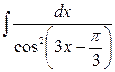 ; в)
; в) 
Основные методы интегрирования.
Дата добавления: 2015-10-16; просмотров: 701 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Количество часов на учебную и производственную практику | | | Метод интегрирования подстановкой (заменой переменной) |