Способи розв’язання задач

В даний час головним результатом сучасної математики є повне переосмислення її традиційних областей, раніше доведених теорем і вирішених завдань. Тому представляє інтерес розглянути сучасні додатки класичної задачі Аполлонія. Інверсія як потужний інструмент геометрії дозволяє виконати лаконічні вирішення даної задачі [6].

Дотримуючись принципу наочності, ми розглянули сучасні додатки завдання Аполлонія в програмі «Жива геометрія», яка надає для цього всі необхідні засоби: створення точно накреслених креслень, побудова й зміна геометричних об'єктів, плавну зміну положення вихідних об'єктів [3]. Нами були розроблені інструменти користувача, що дозволяють автоматично побудувати образи точок, прямих і кіл при інверсії. Дані інструменти послужили базою для вирішення завдання Аполлонія в програмному середовищі «Жива геометрія».

Аполлоній Пергський є одним з трьох (поряд з Евклідом і Архімедом) великих геометрів античності, що жили в III столітті до н. е.. Серед його численних робіт особливе місце займає вирішення задачі про побудову кола, що стосується трьох заданих кіл [1]. Пізніше її досліджували багато математики, включаючи Леонарда Ейлера.

Оскільки три кола на площині можна розташувати різними способами, деякі з яких ми представили на рис. 1, розглянемо окремі випадки завдання Аполлонія. Наведемо побудова одного з них.

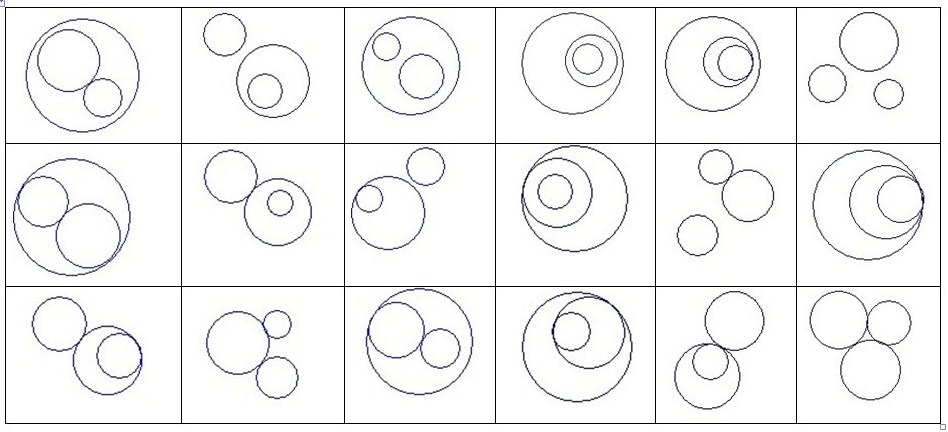
рис.1.

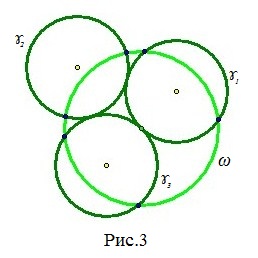
Зобразимо три кола ɤ1, ɤ2, ɤ3, що стосуються один одного (рис.2). Застосуємо інверсію відносно допоміжного кола ω з центром в точці дотику кіл ɤ1 і ɤ3 довільним радіусом (рис.3). Можемо використовувати створені нами інструменти користувача [5], що дозволяють будувати образ кіл перетинають інверсивне коло ω в двох точках, що проходять і не проходять через її центр у програмі «Жива геометрія». Застосування цих інструментів дозволяє позбутися від зайвих ліній, автоматично ладу потрібний образ.

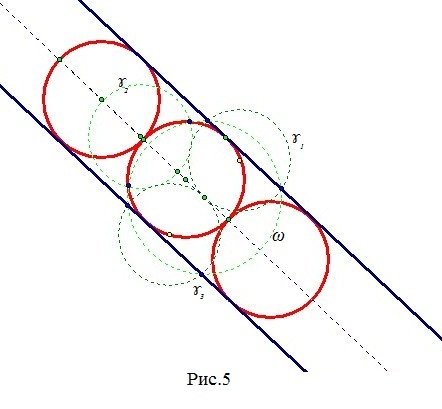
Тоді за властивостями інверсії окружності ɤ1 і ɤ3перейдут в паралельні прямі, коло ɤ2-в коло, що стосується даних прямих (рис.4).

Якщо дано дві паралельні прямі і коло, що стосується кожної прямої, то потрібна побудова кола, яка стосується всіх трьох даних ліній. Рішенням цього завдання будуть 2 кола, представлені на малюнку 5.

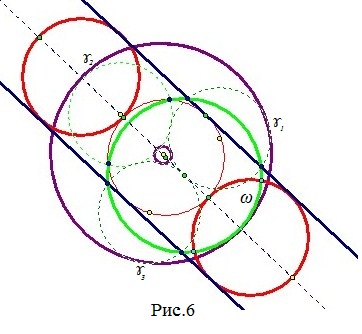
Так як умову задачі інваріантно щодо перетворення інверсії, то рішення вихідної задачі можемо отримати, Інвертуємо назад дані елементи (застосуємо інструменти користувача). Рішенням будуть кола з малим і великим радіусом (рис.6).

Сховаємо всі зайві елементи, залишивши видимими дані і шукані кола (рис.7). Задача розв'язана.

Дата добавления: 2015-10-16