Поверхностное натяжение. Смачивание. Капиллярные явления.

Жидкое состояние возникает тогда, когда потенциальная энергия взаимодействия молекул оказывается большеих кинетической энергии. Силы притяжения между молекулами в жидкостях весьма значительны и обеспечивают удержание молекул в определенном объеме. Таким образом, у жидкости образуется поверхность, которая ограничивает ее объем.

На молекулы, находящиеся внутри жидкости, силы взаимного притяжения действуют в разных направлениях,и их результирующее действие стремится к нулю. Если же молекула находится в тонком приповерхностном слое (рис. 8.2.1) толщиной r порядка нескольких эффективных диаметров молекул, то на нее будет действовать некомпенсированная (из-за много меньшей плотности молекул насыщенного пара вне жидкости) результирующая сила, направленная перпендикулярно поверхности внутрь жидкости.

Если мы будем увеличивать поверхность жидкости, томы будем вынуждены ввести в приповерхностный слой новые молекулы. Но при этом надо совершить работу против сил, действующих в приповерхностном слое. Таким образом, потенциальная энергия жидкости должна увеличиться. Следовательно, потенциальная энергия, связанная с поверхностью жидкости, должна быть пропорциональна площади этой поверхности. При изотермических условиях роль потенциальной энергии играет свободная энергия F (потенциал Гельмгольца). Итак, ясно, что F~S или иначе F=σS где σ = F/S - удельная плотность свободной энергии поверхности.

Так же, как в механике, система стремится достигнуть состояния с наименьшей потенциальной энергией (устойчивое равновесие), в термодинамике система стремится к минимуму свободной энергии. Таким образом, жидкость стремится приобрести такую форму, чтобы ее поверхность для данного объема была минимальной. Итак, поверхность жидкости стремится сократиться, но это можно трактовать как наличие некоторых сил поверхностного натяжения. Это обстоятельство приводит к тому, что маленькие капли жидкости или жидкость в невесомости принимают форму шара. Наличие поверхностного натяжения эффектно демонстрируется с помощью мыльной пленки (рис.8.2.2). Площадь поверхности мыльной пленки dS = 2ldx (2 - т.к. две пленки с обеих сторон).

, (8.2.1.)

откуда - сила, отнесенная к единице длины поверхности, действует вдоль поверхности, поэтому σ называется также поверхностным натяжением.

Итак, поверхностное натяжение равно плотности свободной энергии. Поверхностная энергия, очевидно, зависит от свойств той среды, с которой соприкасается поверхность жидкости, а, значит, и поверхностное натяжение тоже. Поэтому для корректного описания поверхностного натяжения надо учитывать пару соприкасающихся объектов при Т = 293 К

σ_{вода-эфир} = 0,0122 Н/м; σ_{вода-бензол} = 0,0336 Н/м;

σ_{ртуть-воздух} = 0,465 Н/м; σ_{ртуть-вода} = 0,427 Н/м.

Рассмотрим условия равновесия на границе раздела двух жидкостей. Если на поверхность одной жидкости поместить каплю другой, более легкой (чтобы не тонула) жидкости, то возможны два результата, в зависимости от соотношения поверхностных натяжений жидкости (рис. 8.2.3):

1) если σ₁₃ < σ₂₁ + σ₃₂, то капля останется каплей, а углы Θ₁ и Θ₂ будут определяться краевыми уравнениями, вытекающими из условия равновесия, т.е. из условия равенства равнодействующей всех сил, действующих на элемент поверхности dl, перпендикулярный плоскости рис. 8.1.3.;

(8.2.2)

2) если s₁₃>s₂₁+s_{32 ,} то капля растечется по поверхности жидкости, т.к. равновесная ситуация, реализуемая в предыдущем случае, невозможна.

Расмотрим условия равновесия на границе жидкость-твердое тело. Возможны три ситуации (рис. 8.2.3).

1) Полное несмачивание: условие равновесия в этом случае имеет вид s₁₃>s₂₁ cosa+s_{32 .}

2) Частичное смачивание: условие равновесия реализуется в том же виде.

3) Полное смачивание: условие равновесия не реализуется, жидкость растекается по поверхности твердого тела молекулярным слоем.

Из-за смачивания или несмачивания поверхность жидкости вблизи вертикальной стенки сосуда искривляется по-разному (рис. 2.8.4). Таким образом, силы поверхностного натяжения, возникающие при взаимодействии жидкости со стенкой вертикального сосуда, стремятся либо поднять, либо опустить уровень жидкости.

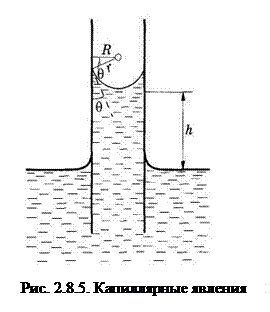
Это явление особенно наглядно проявляется в капиллярных (узких трубках) (рис. 2.8.5).

Поскольку отношение длины периметра столба жидкости к площади поверхностного сечения будет тем больше, чем меньше будет радиус цилиндрического сосуда, то, соответственно, и проявление сил поверхностного натяжения будет сказываться заметнее на фоне силы тяжести. Поэтому в трубках малого диаметра (капиллярах) эти эффекты проявляются сильнее.

Для вывода зависимости высоты поднятия жидкости в капилляре от параметров капилляра и жидкости рассмотрим, предварительно, как связано дополнительное давление, обусловленное действием сил поверхностного натяжения, с радиусом кривизны поверхности. Для этого рассмотрим мыльный пузырь (рис. 8.2.6), давление внутри которого превышает атмосферное на некоторую величину . Последнее обусловлено действием сил поверхностного натяжения. Если давление внутри пузыря увеличить, то его размеры тоже увеличатся (r ® r+dr) и, соответственно, возрастет объем на dV=4pr²dr. При этом совершается работа против сил натяжения

δA’ = Dр_лdV = Dр_л4p r²dr. (8.2.3)

Эта работа приведет к увеличению свободной энергии поверхности, т.е.

δA’ = dF = sdS, где dS=2d(4p r²) = 2×8prdr (здесь dS = 2d(4p r²),

т.к. увеличивается и внутренняя, и внешняя поверхности пузыря.

Итак,

Dр_л4p r²dr = 16prdrs и Dр_л = 2×(2s/r). (8.2.4)

Давление Dр_л – создается двумя изогнутыми поверхностями. Поэтому давление под одной искривленной поверхностью

Dр_л = 2s/r. (8.2.5)

В общем случае несферической поверхности

Dр_л =s (1/r₁+1/r₂) (8.2.6)

формула Лапласа, где r₁, r₂ – главные радиусы кривизны. Условие равновесия в капилляре запишем в виде:

rgh = Dр_л = 2s/r. (8.2.7)

С учетом того, что R= r cosq, откуда r= R/cosq; получим

rgh = 2cosqs/R, (8.2.8)

где R – радиус капилляра.

Таким образом,

H = 2 cosqs/Rgh, (8.2.9)

т.е. h ~ 1/R.

В заключение параграфа отметим, что если жидкость неоднородна и в ее составе есть компоненты с разным значением поверхностного натяжения, то из условия минимума свободной энергии следует, что жидкость с меньшим s вытесняется на поверхность смеси жидкостей. Именно этим, например, объясняется то, что раствор мыла оказывается на поверхности воды. Последнее же объясняет относительную устойчивость мыльной пленки (молекулы воды оттесняются от поверхности).

Дата добавления: 2015-10-21