Гемодинамика и реология сосудистых поражений: применение в диагностике и лечении

Хирург, который стоит перед проб-
лемой заболевания сосудов, должен
основывать свои решения на комп-
лексной оценке гемодинамических
и реологических факторов.

Нормальный кровоток. Основные
потери энергии крови при ее дви-
жении, выражающиеся в возникаю-
щем градиенте давления, связаны с
вязкостью и скоростью.

При наличии прямой, ригидной
цилиндрической трубки с постоян-
ным ламинарным током жидкости
вязкость ответственна за все энер-
гетические потери. Уравнение Пуа-
зейля определяет взаимоотноше-
ния между градиентом давле-
ния (энергии) и током жидкости
при вышеназванных строгих усло-
виях:

где P₁ — давление на входе; Р₂ —
давление на выходе; О — объемный
кровоток, равный Vпr²; L — длина,
n — коэффициент вязкости в пуа-
зах; r — радиус просвета сосуда.

Это равенство утверждает, что
при постоянном кровотоке гради-
ент давления прямо пропорциона-
лен длине сегмента и вязкости кро-
ви и обратно пропорционален чет-
вертой степени радиуса сегмента.
Среди многих факторов, определя-
ющих вязкость крови, гематокрит
является важнейшим; при цифрах,
равных 50 %, вязкость крови повы-
шается вдвое по сравнению с тако-
вой при гематокрите 35 %. Таким
образом, в ситуациях, когда преоб-
ладает ламинарный ток крови, ге-
матокрит может оказывать значи-
тельный эффект на градиент давле-
ния или кровоток.

Реальные условия движения кро-
ви далеки от описанных выше, по-
этому всякий раз, когда меняется
направление движения, возникают
дополнительные потери энергии
крови. Это происходит при любом
изгибе сосуда, его раздвоении или
ответвлении и всегда — при его су-
жении или расширении. С каждой
систолой сердца поток крови уско-
ряется и замедляется, вплоть до
движения в обратном направлении
во время диастолы, движется к
стенкам сосуда при его расшире-
нии и обратно — при сужении его
просвета. Инерционные потери
пропорциональны плотности кро-
ви и квадрату изменений ее скоро-
сти:

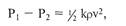
где к — постоянная; р — плотность
крови; v — скорость движения кро-
ви.

Во многих ситуациях инерцион-
ные потери даже больше, чем поте-
ри, связанные с вязкостью крови.

Относительные вклады вязкости
и инерционных потерь в кровоток
варьируют в значительных преде-
лах, поэтому очевидно, что невоз-
можно охарактеризовать кровоток с
помощью простой формулы даже
при нормальных условиях. Тем не
менее можно выразить общую кон-
цепцию вклада этих величин фор-
мулой:

в которой сохраняются все выше-
приведенные обозначения.

В связи с тем что сопротивление
(R) крови в сегменте сосуда — это
отношение градиента давления и
кровотока через сегмент (AP/Q), а
v=Q/pr², сопротивление обратно
пропорционально четвертой степе-
ни радиуса:

В этой формуле сохраняются все
вышеприведенные обозначения.

Формула также отражает тот факт,
что сопротивление не является по-
стоянной величиной и возрастает с
увеличением кровотока. Таким об-
разом, сопротивление участка сосу-
да может быть определено только
при точно известных объеме крово-
тока, частоте пульса и других фак-
торах, однако минимально возмож-
ное сопротивление можно вычис-
лить, основываясь на законе Пуа-
зейля, хотя следует понимать, что
истинное сопротивление всегда бу-
дет выше, чем рассчитанное мини-
мальное.

Дата добавления: 2015-10-21