
Читайте также:
|
(построение гистограммы )
Экспериментальные исследования погрешностей средств измерений различных типов показали, что существует много законов распределения погрешностей, причем часто они существенно отличаются от гауссовского. Поскольку знание реального закона распределения необходимо для выбора методики получения оценки измеряемой величины, то в необходимых случаях приходится выбирать закон распределения, в наибольшей мере соответствующей эксперимсентальным данным – идентифицировать форму закона распределения. Исходные данные для выбора закона распределения получают из гистограммы, т.е. экспериментально построенного графика статистического распределения погрешностей.
Задача. Произвести статистическую обработку ряда наблюдений измеряемой величины X1; X2; X3; … Xn-1; X n. Выявить и исключить промахи в результатах наблюдений. Определить значение результата измерения, предполагая отсутствие систематической погрешности, с учетом малого числа измерений одной и той же физической величины (использовать при этом критерий Стъюдента). Определить случайную среднеквадратическую погрешность среднеарифметических значений серии измерений  . Построить гистограмму результатов наблюдений и высказать гипотезу о предполагаемом законе распределения случайных погрешностей.
. Построить гистограмму результатов наблюдений и высказать гипотезу о предполагаемом законе распределения случайных погрешностей.
Рассмотрим на примере варианта № 30.
Набор ряда наблюдений: 488, 495, 494, 496, 546, 498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505, 524, 509, 508, 493, 511, 518, 522, 503.
Доверительная вероятность  = 0,9011.
= 0,9011.
Решение: рассмотрим на примере варианта 30.
1. Объем ряда наблюдений составляет n = 28.
2. Исключаем из заданного ряда наблюдений грубые ошибки– промахи. Для этого найдём:
а) среднеарифметическое значение (мат. ожидание) результатов наблюдения

| (1) |
где n – общее число наблюдений;
б) абсолютные погрешности каждого наблюдения
 ; ;
| (2) |
-15,25; -8,25; -9,25; -7,25; 42,75; -5,25; 4,75; -20,25; -26,25; -3,25; -16,25; 3,75; -6,25; 19,75; -0,25; -10,25; 4,75; -1,25; -10,25; 1,75; 20,75; 5,75; 4,75; -10,25; 7,75; 14,75; 18,75; -0,25.
в) среднеквадратическое значение (СКО) одного ряда измерения

| (3) |
г) обнаруживаем грубую ошибку (промах) по критерию Δ xi ≥ 3σ1 и исключаем этот(и) результат(ы) из ряда измерений.
Примечание: 1. Следует обратить внимание, что критерий 3σ справедлив для заданной доверительной вероятности P = 0,997, если доверительная вероятность P = 0,95, то критерий равен 2σ, а при P = 0,9 − критерий равен 1,65σ.
Если в условии задачи доверительная вероятность не задана, то её следует самостоятельно принять равной 0.997.
При выполнении задания значение доверительной вероятности (функции Лапласа) указано для каждого варианта задачи во втором столбце таблицы с заданиями, а коэффициент ширины доверительного интервала z выбираетсяпо таблице П.1 в приложении. Тогда критерий обнаружения промаха будет равен zσ.
3. После определения СКО следует определить критерий промаха. По таблице П. 1 для  = 0,9011 (по заданию) определяем критерий обнаружения промаха
= 0,9011 (по заданию) определяем критерий обнаружения промаха
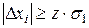 =1,65 =1,65  =23,74. =23,74.
| (4) |
Выполняя сравнение, определяем, что указанному условию (4) не удовлетворяет значение  = 42,75, которому в исходной последовательности соответствует число 546 – исключаем его из ряда измерений.
= 42,75, которому в исходной последовательности соответствует число 546 – исключаем его из ряда измерений.
4. Записываем ряд наблюдений, оставшийся после исключения грубых ошибок:
488, 495, 494, 496, 498, 508, 483, 477, 500, 487, 507, 497, 523, 503, 493, 508, 502, 493, 505, 524, 509, 508, 493, 511, 518, 522, 503.
Теперь объем ряда составляет n = 27.
5. На основании оставшегося ряда измерений повторно определяем 
 . .
|
6. Используя выражение (2), определяем абсолютные погрешности  :
:
-13,67; -6,67; -7,67; -5,67; -3,67; 6,33; -18,67; -24,67; -1,67; -14,67; 5,33; -4,67; 21,33; 1,33; -8,67; 6,33; 0,33; -8,67; 3,33; 22,33; 7,33; 6,33; -8,67; 9,33; 16,33; 20,33; 1,33.
7. Используя выражение (3), определяем СКО для нового ряда
 =11,9228. =11,9228.
|
8. Для полученного значения СКО новый критерий промаха составит  =19,67. Этому критерию не удовлетворяют значения
=19,67. Этому критерию не удовлетворяют значения  = 21,33; 22,33 и 20,33. Этим значениям соответствуют результаты 523, 524 и 522 – исключаем их из ряда измерений.
= 21,33; 22,33 и 20,33. Этим значениям соответствуют результаты 523, 524 и 522 – исключаем их из ряда измерений.
9. Вновь запишем получившийся ряд:
488, 495, 494, 496, 498, 508, 483, 477, 500, 487, 507, 497, 503, 493, 508, 502, 493, 505, 509, 508, 493, 511, 518, 503.
n = 24.
10. Пункты 5–9 выполняются до тех пор, пока не будут исключены все грубые ошибки, при этом каждый раз определяем 
Продолжая поиск промахов получаем:
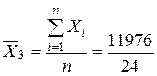 = 499;
= 499;
 : -11,00; -4,00; -5,00; -3,00; -1,00; 9,00; -16,00; -22,00; 1,00; -12,00; 8,00; -2,00; 4,00; -6,00; 9,00; 3,00; -6,00; 6,00; 10,00; 9,00; -6,00; 12,00; 19,00; 4,00;
: -11,00; -4,00; -5,00; -3,00; -1,00; 9,00; -16,00; -22,00; 1,00; -12,00; 8,00; -2,00; 4,00; -6,00; 9,00; 3,00; -6,00; 6,00; 10,00; 9,00; -6,00; 12,00; 19,00; 4,00;
 =9,68;
=9,68;
 =15,98, не удовлетворяют значения
=15,98, не удовлетворяют значения  = 19, исключаем значение 518:
= 19, исключаем значение 518:
488, 495, 494, 496, 498, 508, 483, 477, 500, 487, 507, 497, 503, 493, 508, 502, 493, 505, 509, 508, 493, 511, 503.
n = 23.
 = 498,17;
= 498,17;
 : -10,17; -3,17; -4,17; -2,17; -0,17; 9,83; -15,17; -21,17; 1,83; -11,17; 8,83; -1,17; 4,83; -5,17; 9,83; 3,83; -5,17; 6,83; 10,83; 9,83; -5,17; 12,83; 4,83;
: -10,17; -3,17; -4,17; -2,17; -0,17; 9,83; -15,17; -21,17; 1,83; -11,17; 8,83; -1,17; 4,83; -5,17; 9,83; 3,83; -5,17; 6,83; 10,83; 9,83; -5,17; 12,83; 4,83;
 =8,99;
=8,99;
 =14,84 – промахов не обнаружено.
=14,84 – промахов не обнаружено.
Таким образом, для указанного варианта для исключения всех промахов потребовалось 4 итерации поиска.
11. Из оставшихся результатов наблюдения выстраиваем вариационный ряд, т.е. располагаем результаты в прядке возрастания их значений и выбираем минимальное  и максимальное
и максимальное  значения – крайние члены вариационного ряда.
значения – крайние члены вариационного ряда.
477; 483; 487; 488; 493; 493; 493; 494; 495; 496; 497; 498; 500; 502; 503; 503; 505; 507; 508; 508; 508; 509; 511;
 =477;
=477;  =511.
=511.
12. Разбиваем вариационный ряд на r – число равных интервалов – бинов. Число интервалов r определяется числом измерений n и может быть выбрано на основании табл. №1.2., рекомендованной ВНИИМ [1, 120 ].
Таблица №1.2.
| n | r |
| < 30 | 5 – 8 |
| 30 – 100 | 7 – 9 |
| 100 – 500 | 8 – 12 |
| 500 – 1000 | 10 – 16 |
| 1000 – 10000 | 12 – 22 |
Выберем r = 6.
13. Ширина бинов определяется по формуле
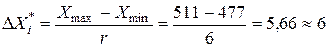
| (5) |
Следует соблюдать некоторую осторожность при выборе ширины бинов  для гистограммы. Если бины выбрать слишком широкими, то все (или почти все) отсчеты попадут в один бин и гистограмма выродится в малоинтересный единственный прямоугольник. Если же бины выбраны слишком узкими, то лишь небольшое их число будет содержать более чем один отсчет и гистограмма будет состоять из большого числа узких прямоугольников, почти одинаковой высоты. Масштабы по осям гистограммы должны быть такими, чтобы отношение её высоты к основанию примерно было равно 5:8.
для гистограммы. Если бины выбрать слишком широкими, то все (или почти все) отсчеты попадут в один бин и гистограмма выродится в малоинтересный единственный прямоугольник. Если же бины выбраны слишком узкими, то лишь небольшое их число будет содержать более чем один отсчет и гистограмма будет состоять из большого числа узких прямоугольников, почти одинаковой высоты. Масштабы по осям гистограммы должны быть такими, чтобы отношение её высоты к основанию примерно было равно 5:8.
Примечание: Рассчитанное значение ширины бинов округляем до целого числа.
14. Определяем границы интервалов между выбранными бинами

| (6) |
Получим: 477, 483, 489, 495, 501, 507.
15. Подсчитываем частоты  попадания результатов в каждый из выделенных интервалов, равные числу результатов, лежащих в каждом i – интервале, т.е. меньших или равных его правой и больших левой границы
попадания результатов в каждый из выделенных интервалов, равные числу результатов, лежащих в каждом i – интервале, т.е. меньших или равных его правой и больших левой границы


Этим правилом следует руководствоваться, чтобы граничные результаты дважды не попали в соседние бины.
Получаем  : 1, 3, 4, 5, 4, 6.
: 1, 3, 4, 5, 4, 6.
16. Вычисляем вероятности попадания значений вариационного ряда в каждый из выделенных интервалов

| (7) |
где n – общее число наблюдений, оставшихся после исключения промахов.
Получаем:  = 0,0434; 0,1304; 0,1739; 0,2173; 0,1739; 0,2608.
= 0,0434; 0,1304; 0,1739; 0,2173; 0,1739; 0,2608.
17. Если теперь разделить полученные оценки вероятностей  на длину интервала, то получим величины, являющиеся оценками средней плотности распределения вероятности в интервале
на длину интервала, то получим величины, являющиеся оценками средней плотности распределения вероятности в интервале 

| (8) |
Получаем:
 = 0,0072 = 7,3*10-3;
= 0,0072 = 7,3*10-3;
 = 0,0217 = 21,7*10-3;
= 0,0217 = 21,7*10-3;
 = 0,0289 = 28,9*10-3;
= 0,0289 = 28,9*10-3;
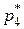 = 0,0362 = 36,2*10-3;
= 0,0362 = 36,2*10-3;
 = 0,0289 = 28,9*10-3;
= 0,0289 = 28,9*10-3;
 = 0,0434 = 43,4*10-3.
= 0,0434 = 43,4*10-3.
Полученные результаты следует свести в следующую таблицу.
Таблица №1.3.
| № | 
| 
| 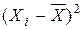
| Вариац. ряд | Границы бинов | № бинов | 
| 
| 
|

| 
| 
| |||||||

| 
| 
| m1 | 
| 
| ||||

| |||||||||

| 
| 
| 
| 
| |||||

| 
| ||||||||

| 
| 
| 
| r | mr | 
| 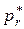
| ||
| n | 
| 
| 
|
18. Откладываем вдоль оси абсцисс интервалы  в порядке возрастания индекса i и на каждом интервале строим прямоугольник с высотой равной
в порядке возрастания индекса i и на каждом интервале строим прямоугольник с высотой равной  Полученный график (см. рис.1.5.) называется гистограммой статистического распределения погрешностей измерения. Форма полученной гистограммы позволяет сделать вывод о предполагаемом законе распределения погрешностей измерения.
Полученный график (см. рис.1.5.) называется гистограммой статистического распределения погрешностей измерения. Форма полученной гистограммы позволяет сделать вывод о предполагаемом законе распределения погрешностей измерения.
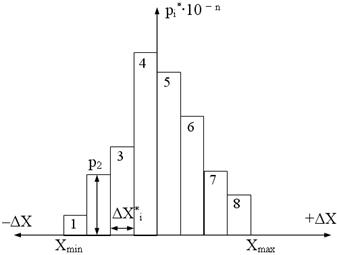 Рис. 1.5. Гистограмма статистического распределения погрешностей измерения
Рис. 1.5. Гистограмма статистического распределения погрешностей измерения
|  Рис. 1.6. Гистограмма для варианта 30
Рис. 1.6. Гистограмма для варианта 30
|
По форме гистограммы можно высказать предположение о «нормальном» (гауссовском), «равномерном», «треугольном» или «законе арксинуса» (см.[4], раздел «Другие виды распределения случайных погрешностей»).
Примечание: при построении графика следует указать масштабы по оси абсцисс и оси ординат, а также надписать каждый прямоугольник гистограммы. Масштаб по оси абсцисс это
Xmin,  ,
,
т.е. численные значения границ бинов, а по ординате − линейный масштаб, максимальное значение которого выбирается по наибольшему значению  , записанному в таблице 1.3, при этом десятичный множитель выносится в оглавление оси ординат.
, записанному в таблице 1.3, при этом десятичный множитель выносится в оглавление оси ординат.
19. По форме гистограммы необходимо высказать гипотезу о предполагаемом законе распределения случайных погрешностей результата измерений.
20. Вычисляем среднеквадратическое отклонение среднеарифметических значений k – серии рядов по n измерениям одной и той же физической величины
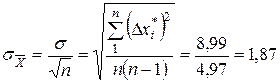
| (9) |
где  среднеквадратическое отклонение единичного ряда измерений, найденное после исключения всех промахов,
среднеквадратическое отклонение единичного ряда измерений, найденное после исключения всех промахов,  абсолютная погрешность каждого результата единичного ряда из n измерений.
абсолютная погрешность каждого результата единичного ряда из n измерений.
Примечание: Если бы производили k- серий измерений одной и той же величины по n измерений в каждом ряду, то полученные средне-арифметические значения  имели бы некоторый разброс относительно мат. ожидания
имели бы некоторый разброс относительно мат. ожидания 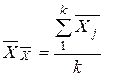 этих среднеарифметических величин. При этом, как показано в теории погрешностей, этот разброс в
этих среднеарифметических величин. При этом, как показано в теории погрешностей, этот разброс в  раз меньше разброса отдельных измерений от среднеарифметического значения единичного ряда измерений.
раз меньше разброса отдельных измерений от среднеарифметического значения единичного ряда измерений.
11. Записываем результат измерения (если n < 50) в следующем виде
 = 498,17 ± 1,31*1,87 = 498,17 ± 2,44, = 498,17 ± 1,31*1,87 = 498,17 ± 2,44,
| (10) |
где  коэффициент Стъюдента, зависящий от количества измерений n и заданной доверительной вероятности P, выбирается по таблице 1.4. [3,204] и [1, стр.241] или таб. П.2 в приложении.
коэффициент Стъюдента, зависящий от количества измерений n и заданной доверительной вероятности P, выбирается по таблице 1.4. [3,204] и [1, стр.241] или таб. П.2 в приложении.
Дата добавления: 2015-10-21; просмотров: 179 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Розділ 6. Оцінювання економічної ефективності, реорганізація підприємств | | | ПРИЛОЖЕНИЕ 1 |