Читайте также:
|
Второй замечательный предел
(11)
применяется (как и в случае последовательностей) при вычислении пределов 
, где 
т.е. в случае неопределённости вида 
Следующие три примера решим различными способами.
Пример 34. Вычислить предел функции 
Решение. Находимпределы основания и показателя степени исходноговыражения и убеждаемся в том,что переднаминеопределённость вида Выделяем в исходном выражении формулу 
и вычисляем предел.
Предел выражения можно находить, предварительно вычислив предел его логарифма.
Пример 35. Вычислить предел функции 
Решение. Преобразуем логарифм исходного выражения, применив формулу 
Отсюда 
Теперь находим искомый предел: 
Для вычисления предела 
, где 
т.е. в случае неопределённости вида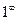 
, можно использовать правило:
. (12)
Пример 36. Вычислить предел функции 
Решение. Находим
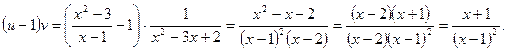
Далее, 
и в силу (12) получаем 
Пример 37. Последовательность функций 
определяется следующим образом: 
Найти 
Решение. Легко заметить и доказать по индукции, что 
Оценим разность между 
и числом 
являющимся корнем уравнения 
. Последнее неравенство следует из того, что 
и 
Применяя полученное неравенство 
к разности 
и т.д., получим 
то есть 
. Отсюда видно, что 
Дата добавления: 2015-10-21; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Предел функции | | | Непрерывность функции |