
Читайте также:
|
Пусть Е- некоторое непустое подмножество множества R действительных чисел, 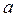 – предельная точка множества Е,
– предельная точка множества Е, 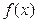 - функция, определённая на Е.
- функция, определённая на Е.
Определение. Число 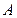 называется пределом функции
называется пределом функции 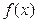 в точке
в точке 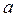 , если
, если
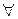 e
e 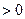
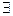 d>0
d>0 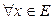
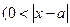
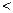 d Þ
d Þ 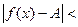 e). (9)
e). (9)
Предел функции в точке 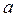 обозначается символом
обозначается символом 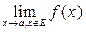 . Во всех рассматриваемых далее примерах функция определена в некоторой проколотой окрестности точки
. Во всех рассматриваемых далее примерах функция определена в некоторой проколотой окрестности точки 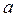 , поэтому мы будем использовать символ
, поэтому мы будем использовать символ 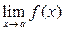 . Определение предела в случае
. Определение предела в случае 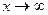 аналогично приведённому (его можно найти в учебнике или конспекте лекций).
аналогично приведённому (его можно найти в учебнике или конспекте лекций).
Определение. Функция 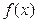 есть бесконечно малая при
есть бесконечно малая при 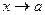 , если
, если 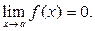
Функции 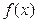 и
и 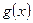 называются эквивалентными (f ~ g) при
называются эквивалентными (f ~ g) при 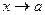 , если в некоторой проколотой окрестности точки а выполнено соотношение
, если в некоторой проколотой окрестности точки а выполнено соотношение 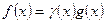 , где
, где 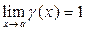 .
.
Определение. Функция 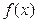 есть бесконечно малая относительно
есть бесконечно малая относительно 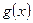 при
при 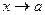 , если в некоторой проколотой окрестности точки а выполнено соотношение
, если в некоторой проколотой окрестности точки а выполнено соотношение 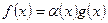 , где
, где 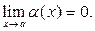 При этом пишут
При этом пишут 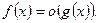 Если при этом g- бесконечно малая, то говорят, что f есть бесконечно малая более высокого порядка по сравнению с g.
Если при этом g- бесконечно малая, то говорят, что f есть бесконечно малая более высокого порядка по сравнению с g.
Справедливы следующие предложения.
1. (f(х) ~ g(х)) при 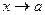
 .
.
2. (f(х) ~ g(х)) при 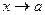
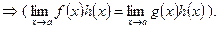
Последнее правило не распространяется на суммы и разности функций, кроме отдельных случаев, например
3. Если f(х) ~ах и g(х) ~bх и 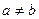 , то (f(х) - g(х)) ~(а- b)х.
, то (f(х) - g(х)) ~(а- b)х.
При вычислении пределов функций полезно использовать таблицу эквивалентных бесконечно малых величин при 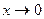 :
:
1. sinx~x, 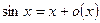 ,
,
2. arcsinx~x, arcsinx =x+o(x),
3. tgx~x, tgx=x+o(x),
4. arctgx ~x, arctgx=x+o(x),
5. 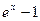 ~x,
~x, 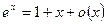 ,
,
6. 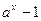 ~xlna,
~xlna, 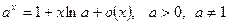 ,
,
7. 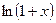 ~x,
~x, 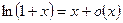 ,
,
8. 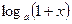 ~
~ 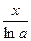 ,
, 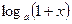
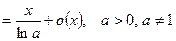 ,
,
9. 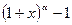 ~
~ 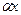 ,
, 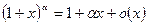 ,
,
10. 1-cosx~ 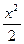 ,
,  .
.
Пример 17. Доказать (найти d(e)), что 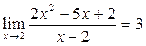 .
.
Решение. Заметив, что квадратный трёхчлен 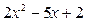 имеет корни
имеет корни 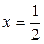 и
и 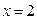 , упростим исходное выражение:
, упростим исходное выражение:
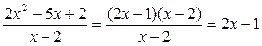 .
.
Тогда соответствующая часть формулы (9) из определения предела функции принимает вид 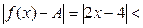 e. Это неравенство будет выполняться, если
e. Это неравенство будет выполняться, если 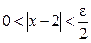 . Следовательно, можно взять
. Следовательно, можно взять 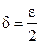 .
.
Пример 18. Найти предел 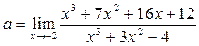 .
.
Решение. При 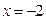 многочлены в числителе и знаменателе исходного выражения обращаются в нуль, следовательно, их пределы в точке
многочлены в числителе и знаменателе исходного выражения обращаются в нуль, следовательно, их пределы в точке 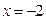 равны нулю и мы имеем неопределённость вида
равны нулю и мы имеем неопределённость вида 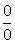 . Преобразуем исходное выражение. Разложим многочлены в его числителе и знаменателе на множители, воспользовавшись тем, что
. Преобразуем исходное выражение. Разложим многочлены в его числителе и знаменателе на множители, воспользовавшись тем, что 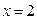 является их корнем, с помощью группировки слагаемых или разделив их на х-2:
является их корнем, с помощью группировки слагаемых или разделив их на х-2:
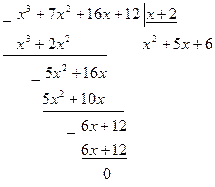
 ,
, 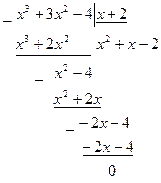 .
.
Получаем 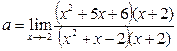
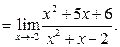 Мы снова имеем неопределённость, так как при х=2 числитель и знаменатель последней дроби обращаются в нуль. Разлагаем их на множители, сокращаем и находим искомый предел:
Мы снова имеем неопределённость, так как при х=2 числитель и знаменатель последней дроби обращаются в нуль. Разлагаем их на множители, сокращаем и находим искомый предел: 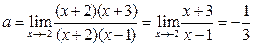 .
.
Пример 19. Найти предел
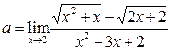 .
.
Решение. Имеем неопределённость вида 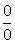 . Преобразуем исходное выражение, умножив его числитель и знаменатель на множитель
. Преобразуем исходное выражение, умножив его числитель и знаменатель на множитель 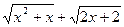 , сопряжённый к числителю.
, сопряжённый к числителю.
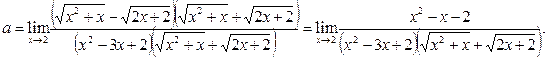
Поскольку 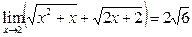 , то
, то
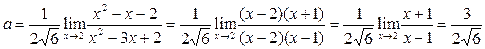 .
.
Пример 20. Найти предел 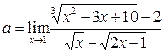 .
.
Решение. Подставив х=1 в выражения в числителе и знаменателе, убеждаемся в том, что имеется неопределённость вида 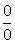 . Воспользуемся формулами (3), (4). Умножим числитель и знаменатель исходного выражения на множитель
. Воспользуемся формулами (3), (4). Умножим числитель и знаменатель исходного выражения на множитель 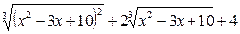 , дополняющий числитель до разности кубов (неполный квадрат суммы), и на множитель
, дополняющий числитель до разности кубов (неполный квадрат суммы), и на множитель 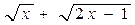 , сопряжённый к знаменателю. Получаем
, сопряжённый к знаменателю. Получаем
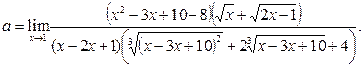 Поскольку
Поскольку 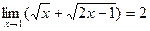 ,
, 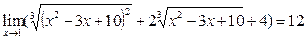 , то
, то
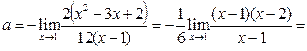
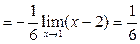 .
.
Пример 20. Найти предел 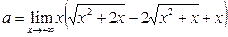 .
.
Решение. Дважды применим приём умножения на сопряжённое выражение.
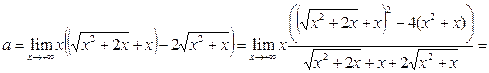
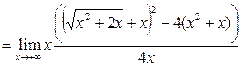 , поскольку
, поскольку 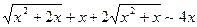 при
при 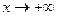 .
.
Далее, 
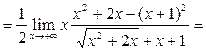
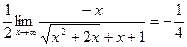 .
.
Пример 21. Найти предел a 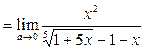 .
.
Решение. Применим формулу (5) 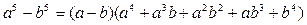 , положив в ней
, положив в ней 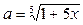 ,
, 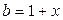 . Умножив числитель и знаменатель исходной дроби на выражение
. Умножив числитель и знаменатель исходной дроби на выражение 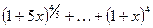 и учитывая, что оно стремится к 5, получаем:
и учитывая, что оно стремится к 5, получаем:
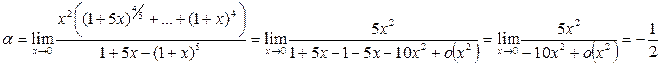
Пример 22. Найти предел 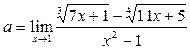 .
.
Решение. 1-й способ. Сделаем замену переменной: 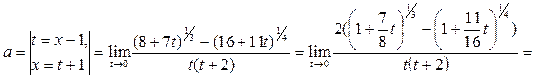

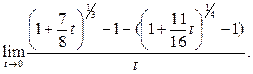 По
По
предложению 3 выражение в числителе эквивалентно 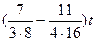 , следовательно,
, следовательно, 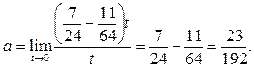
2-й способ. Сделаем замену переменной и воспользуемся формулой 9 из таблицы эквивалентных бесконечно малых.
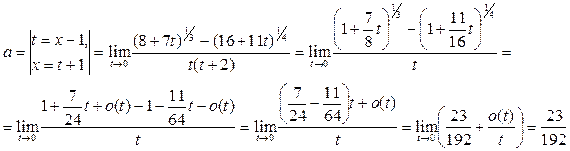
Пример 23. Вычислить предел функции
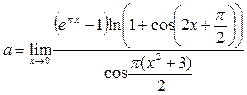
Решение. Воспользовавшись формулами приведения и табличными эквивалентностями, получаем
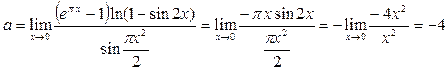
Пример24. Вычислить предел функции
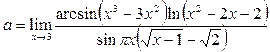 .
.
Решение. Заметив, что все сомножители в числителе и знаменателе исходного выражения есть бесконечно малые при 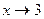 , заменим их, кроме
, заменим их, кроме 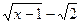 , на эквивалентные:
, на эквивалентные:
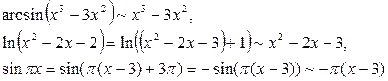
Получаем
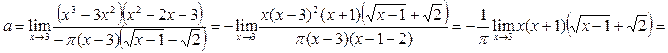
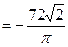 .
.
Пример 25. Вычислить предел функции 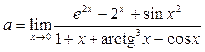 .
.
Решение. 1-й способ. Преобразуем исходное выражение и разделим числитель и знаменатель на х: 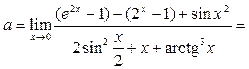
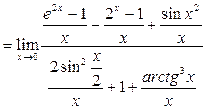 . Тогда по арифметическим свойствам предела
. Тогда по арифметическим свойствам предела 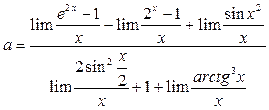 . По таблице заменяем выражения на эквивалентные и переходим к пределу в каждом слагаемом:
. По таблице заменяем выражения на эквивалентные и переходим к пределу в каждом слагаемом: 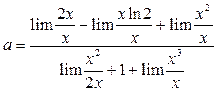
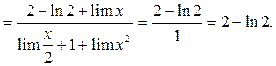
2-й способ. Поскольку 
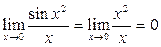 , то
, то 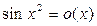 . Точно так же
. Точно так же 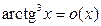 и
и 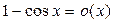 при
при 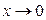 . Воспользовавшись этими соотношениями, получаем
. Воспользовавшись этими соотношениями, получаем
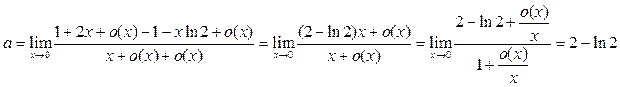 .
.
Пример 26. Вычислить предел функции
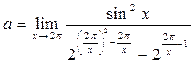 .
.
Решение. Вынесем в знаменателе исходного выражения множитель 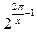 и учтём, что
и учтём, что 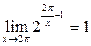 :
: 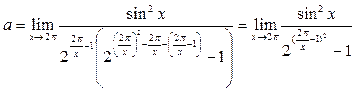 . Теперь сделаем замену переменной, воспользуемся формулой приведения и табличными эквивалентностями:
. Теперь сделаем замену переменной, воспользуемся формулой приведения и табличными эквивалентностями:
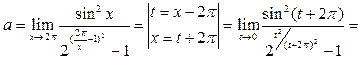
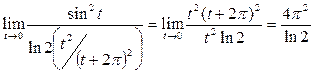 .
.
.
Пример 27. Вычислить предел функции 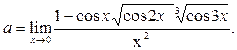
Решение. 1-й способ. Преобразуем числитель исходного выражения:
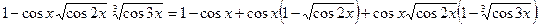
Используя последнее равенство, приём умножения на сопряжённое выражение, предел 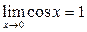 и табличные эквивалентности, получаем:
и табличные эквивалентности, получаем:
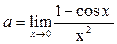 +
+ 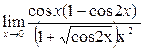 +
+ 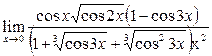 =
=
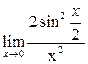 +
+ 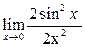 +
+ 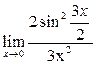 =
= 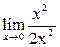 + 1 +
+ 1 + 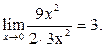
2-й способ. Последовательно используя табличные формулы
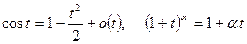 при
при 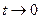 , получаем
, получаем
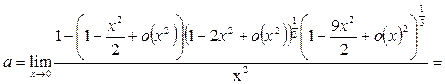
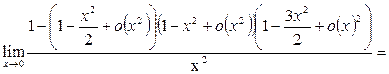
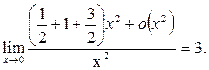
Пример 28. Вычислить предел функции 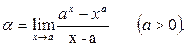
Решение. Сделаем подстановку 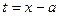 и воспользуемся табличными формулами:
и воспользуемся табличными формулами: 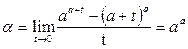
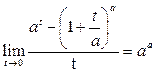
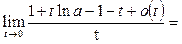
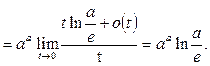
Пример 29. Вычислить предел функции 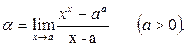
Решение. Сделаем подстановку 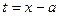 :
:
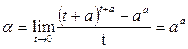
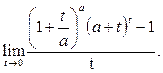 (10)
(10)
Преобразуем выражение 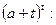
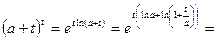
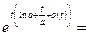
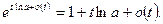
Подставляем полученное выражение в (10):
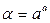
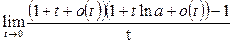
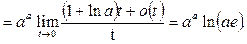
Пример 30. Вычислить предел функции 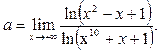
Решение. 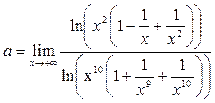
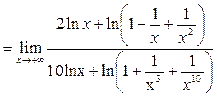
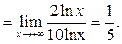
Мы воспользовались свойствами логарифма и тем, что 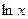 есть бесконечно большая, а
есть бесконечно большая, а 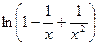 и
и 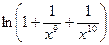 -бесконечно малые при
-бесконечно малые при 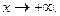
Пример 31. Найти предел 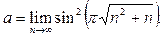
Решение. Понизим степень в исходном выражении и вынесем n из-под корня: 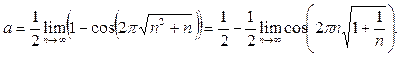 Теперь используем табличное представление
Теперь используем табличное представление 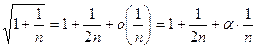 , где
, где 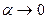 при
при 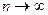 , формулу приведения и то, что
, формулу приведения и то, что 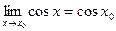 (непрерывность косинуса):
(непрерывность косинуса):
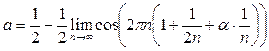
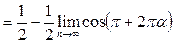
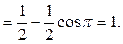
Пример 32. Вычислить предел функции
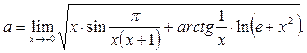
Решение. Величина 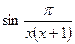 является ограниченной, а x - бесконечно малой при
является ограниченной, а x - бесконечно малой при 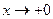 . Поэтому их произведение есть бесконечно малая. Далее,
. Поэтому их произведение есть бесконечно малая. Далее, 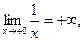
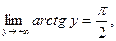 поэтому
поэтому 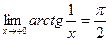 ;
; 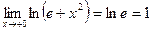 . Отсюда
. Отсюда 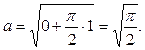
Пример 33. Вычислить предел функции 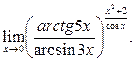
Решение. Воспользуемся тем, что если 
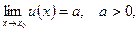
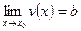 , то
, то 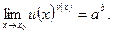 В нашем случае
В нашем случае 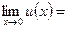
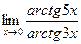 ,
, 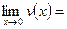
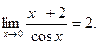 Тогда
Тогда 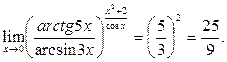
Дата добавления: 2015-10-21; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Предел последовательности | | | Задачи, связанные с применением второго замечательного предела |