Краткая теория. Гироскопом навевается всякое твердое тело, быстро вращающееся вокруг своей оси

Гироскопом навевается всякое твердое тело, быстро вращающееся вокруг своей оси симметрии. Основное свойство гироскопа — способность сохранять неизменным направление оси вращения при отсутствии момента внешних сил.

Гироскопы находят широкое применение в технике. Под гироско­пом в технике обычно понимают симметричный волчок, вращающийся таким образом, что центр тяжести его остается неподвижным, а ось вращения его может занимать любое положение в пространстве. Если гироскоп привести во.вращение вокруг его оси при условии, что эта ось будет вначале неподвижной, то в дальнейшем она бу­дет сохранять свое положение в пространстве. Поэтому такой ги­роскоп можно использовать в качестве указателя неизменного направления при движении судов, самолетов, ракет и т.д. В осно­ве устойчивого движения снаряда, мотоцикла также лежит указанное выше свойство гороскопа.

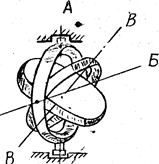
Простейшим гироскопическим прибором является гироскоп в кардановом подвесе, который входит в качестве составной части в большинство существующих гироскопических устройств (рис. 1). В этом гироскопе имеются три оси вращения, они взаимно перпендикулярны и пересекаются в одной точке:

l) ось вращения АА наружного кольца подвеса;

2) ось вращения ББ внутреннего кольца;

ось вращения ВВ ротора гироскопа (ось гироскопа).

Если общий центр тяжести подвижных частей прибора — ротора и двух колец — совпадает с точной пересечения трех осей враще­ния прибора, то такой гироскоп сохраняет равновесие при любом положении его ротора. Тогда гироскоп называется уравновешенным. Равновесие уравновешенного гироскопа в любом положении следует считать безразличным.

Достаточно слегка ударить по одному из колец, чтобы прибор вышел из заданного положения и оставался в некотором новом равновесном положении. Никакой устойчивостью гироскоп не обла­дает, если его ротору не сообщено быстрое вращение. Вели же сообщить ротору гироскопа быстрое вращение и затем ударить по одному из кардановых колец, то можно установить, что гиро­скоп приобрел способность сопротивляться действию усилий, стре­мящихся изменить направление его оси. Гироскоп описанного устройства, в котором существуют три оси вращения, называется гироскопом с тремя степенями свободы.

Если закрепить наружное кольцо неподвижно, то получится прибор с двумя степенями свободы. Если гироскоп с тремя степенями сво­бода обладает свойством устойчивости при быстром вращении, то гироскоп с двумя степенями свободы лишен этого свойства начисто.

Представив себе для простоты, что ротор гироскопа в виде кольца приведен во вращение вокруг оси ZZ в направлении, указанном стрелками.

Тогда его момент импульса будет направлен вдоль оси враще­ния вниз (рис. 2). При повороте оси гироскопа в плоскости рисунка на угол Dj ось займет положение Z₁Z₁ а гироскоп, свя­занный с осью, перейдет в положение X₁YX₁Y₁. Новый вектор момента импульса будет направлен по Z₁Z₁. При этом линейные скорости всех точек кольца, кроме точек X и X₁ изменяют свое направление. В точках X и X₁ скорости лишь смещены параллельно сами себе и векторное изменение скорости D V для них равно нулю. Для точек же Y и Y₁ изменение скорости будет наибольшим, причем, для точки Y₁ — направленным вверх, а для точки Y — будет направлено вниз. Для промежуточных точек кольца изменения скоростей будут лежать в пределах от 0 до ∆V, причем для всех точек половины X₁YX₁ эти изменения направлены вниз, а для точек половины X₁Y₁X₁ — вверх. Вектор момента импульса при изменении положения оси также получил приращение, направленное в плоскости рисунка от прежнего положения оси к новому положению. Согласно правилу моментов это приращение момента импульса может быть вызвано силами, создающими момент в этом направлении, т.е. чтобы вы­звать эти изменения скоростей точек кольца к оси гироскопа надо приложить пару сил F и F₁ лежащих в плоскости, перпендикулярной плоскости рисунка 2 и направленных в соот­ветствии с правилом о направлении момента сил.

Таким образом, если бы ротор не вращался вокруг оси ZZ, то под действием горизонтальных сил F и F₁ он начал бы вра­щаться вокруг оси XX. Если ротор вращается вокруг оси ZZ, то те же самые силы F и F₁ вызывают равномерное вращение ротора вокруг оси YY₁. Этот вывод можно сформулировать в виде общего правила: если приложить к вращающемуся гироскопу пару сил, стремящихся повернуть их вокруг оси XX, перпенди­кулярной к оси вращения гироскопа ZZ, то он будет поворачи­ваться вокруг оси YY₁, перпендикулярной к первым двум. В этом заключается так называемый гироскопический эффект.

Для получения числовой зависимости между скоростью враще­ния гироскопа и моментом приложенных к нему сил рассмотрим движение уравновешенного гироскопа. Движение гироскопа опи­сывается уравнением моментов

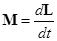, где M — момент внешних сил,

L — момент импульса гироскопа.

Дальнейшие выкладки поясняются рис. 3 и 4: расположение гироскопа и обозначение осей те же, что и на рис. 1,

Пусть вначале М = 0, а гироскоп вращается с угловой скоростью w, так что L = Iw=const (I — момент инерции гироскопа относительно оси вращения). Если затем к оси гироскопа приложить вертикальную внешнюю силу P, то возникнет момент сил М, лежащий в горизонтальной плоскости. Обратившись к уравнению (I) и рис. 3 и 4, нетрудно по­нять, что векторы M и L ортогональны друг другу, а вектор d L направлен так же, как M, поэтому сила P не изменяя величины вектора L, заставляет его конец описывать окружность в горизонтальной плоскости. За время dt проекция вектора L на горизонтальную плоскость повернется на угол dj, причем как следует из (1) и рис. 3

,

где a — угол, который вектор L составляет с вертикалью.

Рис.3 Рис.4

Таким образом, угловая скорость W вращения вектора L равна 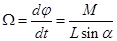, (2)

или в векторной форме [W, L] = M. (2’)

Если ось гироскопа горизонтальна (рис. 4), то вместо (2) получим .

В быстро вращающемся гироскопе направление вектора момента импульса приблизительно совпадает с направлением оси самого гироскопа. Поэтому под действием внешнего момента M ось гироскопа тоже начнет вращаться вокруг вертикальной оси с угло­вой скоростью W, описывая в пространстве конус. Поскольку вектор M поворачивается вместе с L таким образом, что их взаимное расположение не меняется со временем, вращение оси гироскопа при постоянной силе P оказывается равномерным. Это вращение называется регулярной прецессией, а величина W — угловой скоростью прецессии.

Можно сформулировать следующее правило прецессии: под дей­ствием сил, приложенных к оси быстро вращающегося гироскопа и направленных перпендикулярно к этой оси, ось гироскопа прецессирует в плоскости, перпендикулярной к направлению оси.

Направление перемещения точки, в которой приложена сила найдется, если повернуть направление силы на 90° вокруг оси гироскопа в ту сторону, в которую вращается вокруг этой оси ротор гироскопа.

Как уже отмечалось выше, приведенные рассуждения справед­ливы лишь для быстро вращающегося гироскопа, т.е. при

W << w (3)

В этих условиях можно считать, что L = Iw,где I — момент инерции гироскопа относительно его собственной оси вращения. Тогда

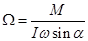(4)

Скажем несколько слов по поводу неравенства (3). Нетрудно видеть, что вектор полного момента импульса гироскопа при наличии прецессии содержит две компоненты: и ,

где I₁ — момент инерции гироскопа относительно его диаметра. Таким образом, вектор полного момента импульса гироскопа L, строго говоря, не совпадает по направлению с вектором угловой скорости w (с осью гироскопа). Этим несовпадением можно, однако, пренебречь при I₁W << Iw. Моменты инерции I и I₁ оказываются в нашем случае величинами одного порядка, в этом случае условием применимости формулы (4) является неравенство (3), которое в обычных гироскопах выполняется очень хорошо (величины W и w отличаются друг от друга, по крайней мере, на три порядка).

Дата добавления: 2015-10-21