Смежность и инцидентность

Пусть v₁, v₂ - вершины, е = (v₁, v₂) - соединяющее их ребро. Тогда вершина v₁ и ребро е инцидентны, вершина v₂ и ребро е также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.

Степенью вершины v графа G(V,E) называется число ребер, инцидентных данной вершине. Обозначение: .

Вершина, имеющая степень 0 называется изолированной, имеющая степень 1 – висячей.

Пример. Для графа, изображенного на рис. 3.5: вершина 3 – изолированная, вершины 1 и 4 - висячие.

Пример. Для графа, изображенного на рис. 3.3.

Ребро e₁ инцидентно вершинам v₁ и v₂. Вершина v₁ инцидентна ребрам e₁ и e₂. Ребра e₁ и e₂ – смежны. Вершины v₁ и v₂ – смежны.

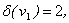
. p(G)=3, q(G)=5.

Т.о. можно заметить, что .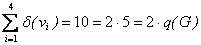

Теорема Эйлера: .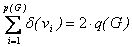

Доказательство данной теоремы вытекает из того, что каждое ребро дает двойной вклад в сумму степеней вершин.

Дата добавления: 2015-10-13