Определения. Графом G(V,E) называется совокупность двух множеств - непустого множества V (множества

Графом G(V,E) называется совокупность двух множеств - непустого множества V (множества вершин) и множества Е неупорядоченных пар различных элемен­тов множества V (Е - множество ребер).

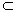G(V,E): , E VxV.

Число вершин графа G обозначим р, а число ребер – q.

р(G) = |V| q(G) = |E|.

Часто рассматриваются следующие родственные графам объекты.

1. Если элементами множества Е являются упорядоченные пары, то граф назы­вается ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества 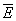- дугами (G(V, )).

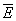2. Если элементом множества Е может быть пара одинаковых (не различных) элементов V, то такой элемент множества Е называется петлей, а граф назы­вается графом с петлями (или псевдографом).

3. Если Е является не множеством, а набором, содержащим несколько одинако­вых элементов, то эти элементы называются кратными ребрами, а граф назы­вается мультиграфом.

Далее выражение: граф G(V,E) означает неориентированный граф без петель и кратных ребер.

Обычно граф изображают диаграммой: вершины - точками (или кружками), ребра - линиями.

Примеры.

1. . .

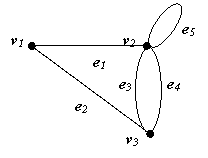
Т.о. это неориентированный граф с петлей и кратными ребрами.

Рис. 3.3. Неориентированный граф с петлей и кратными ребрами.

2. . .

Т.о. это ориентированный граф с петлей и кратными ребрами.

Рис. 3.4. Ориентированный граф с петлей и кратными ребрами.

3. 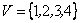. 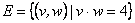, т.о.

Рис. 3.5. Неориентированный граф с петлей.

Дата добавления: 2015-10-13