Кривая Безье

Для построения в программах векторной графики прямых и кривых линий, а также стандартных геометрических фигур используются расчеты координат точек соответствующих фигур по математическим формулам. Для построения кривой линии используются уравнения, описывающие так называемую кривую Безье. Для решения этого уравнения необходимо задать координаты 4 точек Р0, Р1, Р2,Р3.

Лекции - компьютерная графика

Р0, Р1, Р2,Р3 - контрольные точки.

Из четырех контрольных точек кривая Безье проходит только через две - Р0, Р2, поэтому эти точки называются опорными точками. В опорных точках соединяются отдельные кривые друг с другом и образуют единый сложный контур. Две другие контрольные точки - Р1, Р3 – не лежат на кривой, но их расположение на кривизну кривой, поэтому они называются управляющими точками, а линии, которые соединяют управляющие и опорные точки называются управляющими линиями.

Кривая Безье является гладкой кривой, т. е. она не имеет разрывов и непрерывно заполняет участок между начальной опорной точкой и конечной. Управляющие линии являются касательными и касаются кривой Безье в опорных точках. Это позволяет гладко соединить две кривые Безье друг с другом. Управляющие линии при этом расположены вдоль одной прямой.

Рассмотрим пример гладкого соединения двух кривых Безье. Первая кривая - Р0, Р1, Р2,Р3, вторая – Т0,Т1, Т2, Т3.

Лекции - компьютерная графика

Для гладкого соединения нужно конечную точку Р2 первой кривой соединить с начальной точкой Т0 второй кривой, а также необходимо управляющие линии Р3Р2 и Т0Т1 расположить на одной прямой.

Повернем управляющую линию Р2Р3 против часовой стрелки на 180 градусов:

Лекции - компьютерная графика

Изменяя длину управляющих линий, можно выполнять трансформацию:

Лекции - компьютерная графика

Если обе управляющие линии будут лежать на одной прямой:

Лекции - компьютерная графика

Изменение положения хотя бы одной из контрольных точек ведет к изменению формы всей кривой Безье. Из множества элементов кривой Безье составляется сложный контур.

Неоднородный рациональный B-сплайн, NURBS (англ. Non-uniform rational B-spline, читается «нурбс») — математическая форма, применяемая в компьютерной графике для генерации и представления кривых и поверхностей. В общем случае В-сплайн состоит из нескольких сплайновых сегментов, каждый из которых определен как набор управляющих точек. Поэтому коэффициенты многочлена будут зависеть только от управляющих точек на рассматриваемом сегменте кривой. Этот эффект называется локальным управлением, поскольку перемещение управляющей точки будет влиять не на все сегменты кривой. На рисунке показано, как управляющие точки влияют на форму кривой.

В-сплайн с управляющей точкой Р4 в нескольких положениях

Рассмотрим различные виды В-сплайнов.

В-сплайн интерполирует набор из р+1 управляющей точки , и состоит из р-(n-1) сегментов кривой . Кроме того, мы можем определить общий параметр t, нежели отдельный для каждого сегмента в интервале от 0 до 1. Таким образом, для каждого сегмента кривой t будет принадлежать интервалу . Более того, на каждый сегмент будет влиять ровно n управляющих точек от до .

Для каждого i >= n существует узел между и 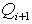для значения t_i параметра t. Для В-сплайна существует p-n-2 узлов. Отсюда исходит понятие однородности: если узлы равномерно распределены на интервале от 0 до 1, т.е. , то говорят, что В-сплайн равномерный. В противном случае – неравномерный. Стоит также обратить внимание на факт, что эти определения касаются узлов, возрастающих по значению, т.е. .

Теперь предположим, что координаты (x, y, z) точки кривой представлены в виде рациональной дроби. В этом случае говорят, что В-сплайн рациональный, иначе – нерациональный:

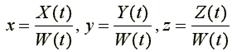
Подводя итог, можно указать на существование 4 типов В-сплайнов:

- равномерные нерациональные;

- неравномерные нерациональные;

- равномерные рациональные;

- неравномерные рациональные.

Последний тип и представляет собой NURBS как наиболее общий случай В-сплайнов.

Теперь рассмотрим математическое описание NURBS. NURBS кривая и поверхность соответственно выражаются следующими двумя параметрическими уравнениями:

где Р_i - управляющая точка, W_i - ассоциированный с ней вес и - базовая функция, определенная рекурсивно следующим образом:

Из формул видно, что точка кривой (поверхности) является средневзвешенной управляющих точек, причем удельный вес каждой точки зависит от одного (двух – для поверхности) параметра.

Следует обратить внимание, что сплайны Безье – это NURBS, у которого веса всех управляющих точек равны 1 и который состоит из 1-го сплайнового сегмента.

Таким образом, NURBS имеет все преимущества Безье-сплайнов, а также следующие:

- возможность локального управления кривизной сплайна;

- наличие весов для управляющих точек, делающих сплайны еще более гибкими.

Единственный недостаток – это несколько более сложное математическое описание NURBS по сравнению с Безье сплайнами, однако порядок этого усложнения не высок.

Дата добавления: 2015-10-13