
Читайте также:
|
Преобразования переноса, масштабирования и поворота в матричной форме
записываются в виде
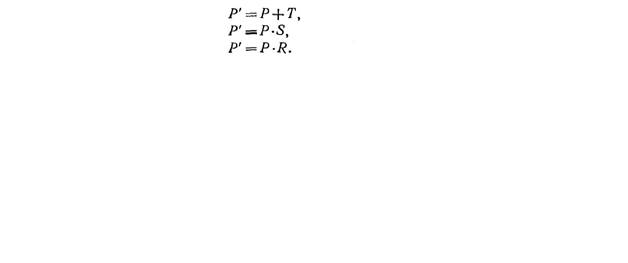

К сожалению, перенос реализуется отдельно (с помощью сложения) от
масштабирования и поворота (с помощью умножения). Хотелось бы представить их таким
способом, чтобы все эти три элементарных преобразования можно было легко объединять
вместе. Ниже в этом разделе показано, как это можно сделать.
Если мы выразим точки в однородных координатах, то все три преобразования
можно реализовать с помощью умножений. Однородные координаты были введены в
геометрии и впоследствии использованы в графике. С однородными координатами и
преобразованиями над ними работают многие пакеты графических подпрограмм и
некоторые дисплейные процессоры. В одних случаях эти координаты используются
прикладной программой непосредственно при задании параметров для графического
пакета, в других — применяются лишь внутри самого пакета и недоступны для
программиста.
В однородных координатах точка Р (х, у) записывается как P(W∙ x, W ∙ y, W) для
любого масштабного множителя W≠0. При этом если для точки задано ее представление в
однородных координатах Р(Х, Y, W), то можно найти ее двумерные декартовы координаты
как x=X/W и y=Y/W. В этой главе W всегда будет равно 1, поэтому операция деления не
требуется. Однородные координаты можно представить как вложение
промасштабированной с коэффициентом W двумерной плоскости в плоскость z=W (здесь
z = 1) в трехмерном пространстве.
Точки теперь описываются трехэлементными вектор-строками, поэтому матрицы
преобразований, на которые умножается вектор точки, чтобы получить другой вектор
точки, должны иметь размер 3x3. Уравнения переноса записываются в виде матрицы
преобразования однородных координат следующим образом:
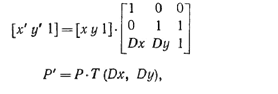
Где
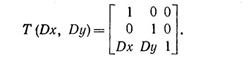
Что будет, если точку Ρ перенести в точку Р' на расстояние (Dx1, Dy1), а затем в Р" на расстояние (Dx2 Dy2). Интуитивно ожидаемый результат в этом случае представляет собой суммарный перенос на расстояние (Dx1+Dx2, Dy1+Dy2). Чтобы доказать это, запишем данные в виде
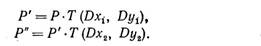
Теперь получим:
Матричное произведение Τ(Dx1, Dy1) ∙ T(Dx2, Dy2) есть


Действительно, результирующий перенос есть (Dx1+Dx2, Dy1+ Dy2). Матричное произведение в разных случаях называют объединением, соединением, конкатенацией и композицией матриц T(Dx1, Dy2) и T(Dx2, Dy2). В этой главе мы будем использоватьтермин композиция.
Уравнения масштабирования в матричной форме записываются в
виде
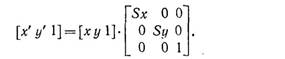
Определяя
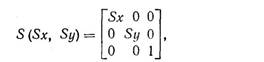
имеем
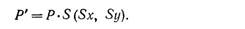
Так же как последовательные переносы являются аддитивными, можно ожидать, что последовательные масштабирования будут мультипликативными. Если заданы
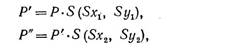
то получим:
Матричное произведение S(Sx1, Sy1)∙S(Sx2, Sy2) есть
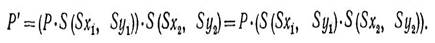
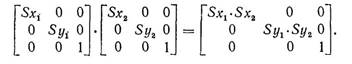
Таким образом, масштабирования в самом деле мультипликативны. И, наконец, уравнения поворота можно представить в виде:


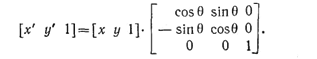
Полагая
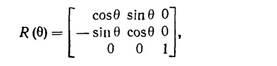
Имеем

Дата добавления: 2015-10-13; просмотров: 132 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Компьютерная геометрия в векторной графике. Построение линий. Однородные координаты. Матричные преобразования. Кривые Безье, NURBS. | | | Кривая Безье |