Важнейшие классы графов

Читайте также:

1. Сколько имеется абстрактных деревьев с 6 вершинами?

6 <<<<<

2. Корневое дерево имеет радиус 4, а у каждой его вершины не более двух сыновей. Каково наибольшее число вершин в таком дереве?

31 <<<<<<

5. В планарном графе семь вершин, из которых три имеют степень 4, остальные степень 5. Сколько граней будет в плоском изображении этого графа?

такого графа не существует<<<<<<

7. Сколько имеется абстрактных двудольных графов с 4 вершинами?

7 <<<<

8. Сколько различных абстрактных двудольных графов можно получить, добавляя одно ребро к графу ?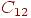

2 <<<<<

9. Какое наименьшее число ребер нужно удалить из графа K6, чтобы получился планарный граф?

3 <<<<<<

1. Дерево имеет две центральные вершины, а его радиус равен 6. Чему равен диаметр этого дерева?

11 <<<<<

16<<<<<<

3. Какие из следующих графов являются двудольными?

----- -- -- --

------ -- --

----- -- -- <<<<<

---- -- <<<<<

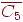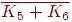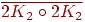4. Какие из следующих графов планарны?

-- -- <<<<<<

-- ---

--- -- <<<<<

-- --

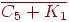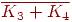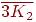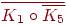5. Какое наименьшее количество новых ребер нужно добавить к графу C6, чтобы получился непланарный граф?

3<<<<<<

2. Сколько различных каркасов имеется у графа ?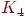

16<<<<<

1. В дереве имеется ровно три листа 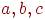, причем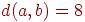 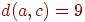, ,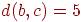. Сколько всего вершин в этом дереве?

12 <<<<<

такого дерева не существует

4. В двудольном графе одна доля состоит из пяти вершин степени 2, а другая из трех вершин, две из которых имеют степень 3. Какова степень третьей вершины?

4 <<<<<<<

такого графа не существует

. Какое наименьшее число ребер нужно удалить из графа K6, чтобы получился двудольный граф?

6 <<<<<

Поиск в ширину.

В процессе выполнения процедуры поиска в ширину вершины графа делятся на новые, открытые и закрытые. Может ли в графе существовать ребро, соединяющее

новую вершину с открытой? <<<<<

открытую вершину с закрытой? <<<<

новую вершину с закрытой?

две открытые вершины? <<<<

Поиск в ширину применяется к графу P3*P3. Какой будет высота BFS-дерева?

2 или 4

2, 3 или 4 <<<<<<<

Для некоторого графа построено BFS-дерево с корнем 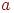. Ребро графа 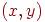дереву не принадлежит. Какие из следующих соотношений могут выполняться ( 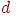обозначает расстояние между вершинами в графе)?

<<<<<

<<<<,

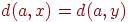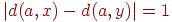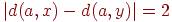
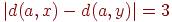
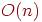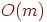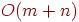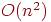Алгоритм поиска в ширину применяется к дереву, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?

<<<<

<<<<<

2. Пусть h - высота BFS-дерева, построенного для графа G. Какие из следующих утверждений верны?

можно выбрать стартовую вершину так, что будет <<<<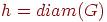

h может быть больше, чем диаметр графа.

можно выбрать стартовую вершину так, что будет <<<<<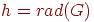

всегда 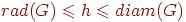<<<<<(3 ответа)

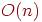
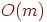
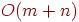
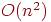Алгоритм поиска в ширину применяется к планарному графу, заданному матрицей смежности. Какие оценки трудоемкости справедливы в этом случае?

<<<<<<

3. В каких из следующих случаев можно утверждать, что путь, соединяющий вершины x и y в BFS-дереве, является кратчайшим путем между ними в графе?

x - корень дерева <<<<

x и y находятся в дереве на одинаковом расстоянии от корня.

x и y - любые вершины.

вершина x является предком вершины y в BFS-дереве.<<<<<

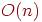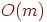
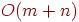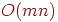
Алгоритм поиска в ширину применяется к планарному графу, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?

<<<<

<<<<<

Для двудольного графа построено BFS-дерево с корнем 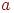. Ребро графа 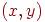дереву не принадлежит. Какие из следующих соотношений могут выполняться ( 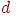обозначает расстояние между вершинами в графе)?

<<<<<<<

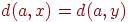
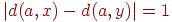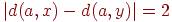
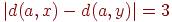
Поиск в глубину.

Алгоритм поиска в глубину применяется к планарному графу, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?

<<<<

<<<<<

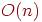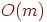
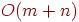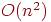2. Для некоторого графа построено DFS-дерево T с корнем a. Ребро графа (x,y) дереву не принадлежит. Какие из следующих соотношений могут выполняться (d обозначает расстояние между вершинами в дереве T)?

<<<<<

<<<<<<

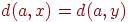
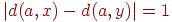
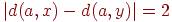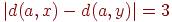3. Для некоторого графа построено DFS-дерево и вычислены глубинные номера вершин. Какие из следующих утверждений верны?

если вершина x не является листом DFS-дерева, то у нее имеется такой сын y, что <<<<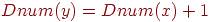

если 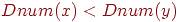то вершина x - предок вершины y в DFS-дереве

если вершина x - предок вершины в DFS-дереве, то <<<<<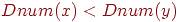

если 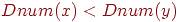и вершины x,y смежны в графе, то вершина x - предок вершины y в DFS-дереве<<<<<

1. Алгоритм поиска в глубину применяется к лесу, заданному списками смежности. Какие оценки трудоемкости справедливы в этом случае?

<<<<<

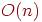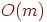
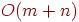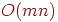
2. Поиск в глубину применяется к графу . Какова будет высота DFS-дерева?

4 -

2 или 4

2, 3 или 4<<<<<<<

3. Какие из следующих утверждений верны?

если вершина x - предок вершины y в DFS-дереве, то <<<<<<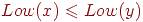

если вершина x - предок вершины y в DFS-дереве, то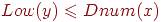

если в графе имеется ребро (x,y), то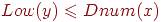

если вершина x - предок вершины y в DFS-дереве и в графе имеется ребро (x,y),то

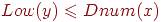
2. Пусть h - высота DFS-дерева, построенного для графа G. Какие из следующих утверждений верны?

всегда -----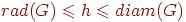

h может быть меньше, чем радиус графа

h может быть больше, чем диаметр графа. <<<<

h не может быть меньше, чем эксцентриситет стартовой вершины.<<<<

Алгоритм поиска в глубину применяется к планарному графу, заданному матрицей смежности. Какие оценки трудоемкости справедливы в этом случае?

<<<<<<

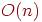
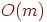
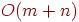
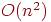. Для двудольного графа построено DFS-дерево T с корнем a. Ребро графа (x,y) дереву не принадлежит. Какие из следующих соотношений могут выполняться (d обозначает расстояние между вершинами в дереве T)?

<<<<<

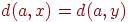
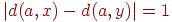
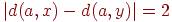
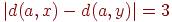Какие из следующих утверждений верны?

лист DFS-дерева не может быть шарниром графа. <<<<<

если (x,y)- обратное ребро, то ни одна отличная от x и y вершина пути, соединяющего x и y в DFS-дереве, не является шарниром

если вершина x является сыном вершины y в DFS-дереве и обе эти вершины - шарниры графа, то ребро (x,y) - перешеек

если (x,y) - обратное ребро, то ни одно ребро пути, соединяющего x и y в DFS-дереве, не является перешейком <<<<<<

Пространство циклов графа.

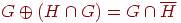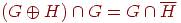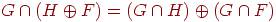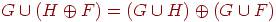
Какие из следующих равенств выполняются для любых графов G, H и F с одним и тем же множеством вершин

<<<

2. Какие из следующих утверждений верны для системы фундаментальных циклов, построенной относительно некоторого каркаса?

каждое ребро каркаса принадлежит точно одному фундаментальному циклу

каждое ребро каркаса принадлежит хотя бы одному фундаментальному циклу

каждое ребро каркаса, не являющееся перешейком, принадлежит хотя бы одному фундаментальному циклу <<

каждое ребро графа, не принадлежащее каркасу, принадлежит точно одному фундаментальному циклу <<

3. Какова будет наибольшая из длин фундаментальных циклов относительно каркаса, построенного с помощью поиска в глубину для графа K3,5?

6 <<<<

4. Какие из следующих утверждений справедливы для любого двусвязного графа?

через любые две вершины проходит простой цикл <<<

через любые два ребра проходит простой цикл <<<<

через любые три вершины проходит простой цикл

через любые три вершины, среди которых имеется хотя бы одна пара смежных, проходит простой цикл <<<<

5. Какие из следующих утверждений верны?

если в графе каждый блок содержит ровно две вершины, то этот граф - дерево

если каждый блок некоторого графа является двудольным графом, то и весь граф двудольный <<<

если каждый блок некоторого графа является планарным графом, то и весь граф планарный <<<

Если в каждом блоке связного графа имеется эйлеров цикл, то и во всем графе есть эйлеров цикл<<<

2. Как может измениться цикломатическое число при добавлении к графу нового ребра?

обязательно увеличивается

увеличивается или не изменяется <<<

может увеличиться, уменьшиться или остаться прежним

если граф связен, то обязательно увеличивается <<<

3. Какова будет суммарная длина фундаментальных циклов относительно каркаса, построенного с помощью поиска в ширину для графа K7?

45 <<<<

5. BC-дерево некоторого графа имеет радиус 2 и содержит 8 вершин, 4 из которых являются листьями. Сколько шарниров у этого графа?

3 <<<<

1. Какие из следующих утверждений верны?

пересечение двух квазициклов - всегда квазицикл

граф, дополнительный к квазициклу - всегда квазицикл

объединение двух квазициклов, не имеющих общих ребер - всегда квазицикл<<<<

если пересечение двух квазициклов - квазицикл, то их объединение - тоже квазицикл<<<<

5. Сколько существует абстрактных связных графов с 5 вершинами, имеющих ровно два блока?

5<<<<

1. G и H - графы с одним и тем же множеством вершин. В графе G 8 ребер, в графе H 9 ребер, а 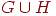в графе 12 ребер. Сколько ребер в графе ?

7 <<<<

4. Какие из следующих утверждений верны?

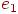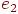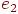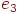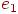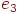если ребро циклически связано с ребром , а ребро циклически связано с ребром , то ребра и циклически связаны <<<<

если вершина 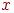циклически связана с вершиной 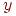, а вершина 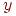циклически связана с вершиной 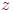, то вершины 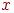и 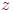циклически связаны

если вершина 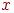циклически связана с ребром 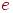, а ребро 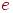циклически связано с вершиной 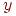, то вершины 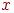и 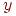циклически связаны <<<<

если ребро 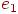циклически связано с вершиной 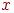, а вершина 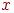циклически связана с ребром 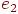, то ребра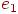

Сколько имеется абстрактных двусвязных графов с 4 вершинами?

3 <<<<

Независимые множества, клики, вершинные покрытия

1. Чему равно кликовое число графа дополнтьельный C9?

4 <<<<

2. Какие из следующих равенств выполняются для любых графов G1 и G2?

***

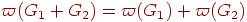
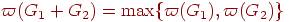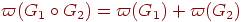
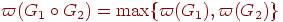3. Сколько листьев будет в дереве подзадач для задачи о независимом множестве, построенном для графа 3K3?

4. Какое наименьшее число ребер нужно добавить к графу K3,5, чтобы получился граф, в котором есть эйлеров цикл?

граф K3,5 невозможно добавлением ребер превратить в граф, имеющий эйлеров цикл.

5. В каких из следующих графов имеется гамильтонов цикл?

K3,3

K3,4

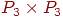
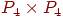
Чему равно число независимости графа Q3?

Дата добавления: 2015-10-13; просмотров: 536 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
МАРШРУТЫ	\|	Что такое эмоциональный интеллект и для чего он нужен

mybiblioteka.su - 2015-2024 год. (0.035 сек.)