
Читайте также:
|
Сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или в другой формулировке: каково максимальное число Ln областей, на которые плоскость делится n прямыми?
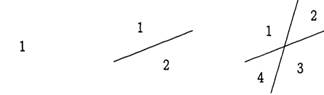
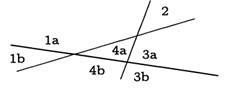
Новая n-я прямая (при n > 0) увеличивает число областей на к тогда и только тогда, когда рассекает k старых областей, а рассекает она к старых областей тогда и только тогда, когда пересекает прежние прямые в k—1 различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать n — 1 старых прямых не более чем в n— 1 различных точках, а значит k<=n и тогда Ln<= Ln-1+n. Более того, легко показать по индукции, что в этой формуле можно достичь равенства. Мы проводим n-ю прямую так, чтобы она не была параллельна никакой другой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
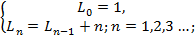 (1.2)
(1.2)
Теперь найдём прямую формулу. Угадать её здесь несколько сложнее (1,2,4,7, 11,16...), поэтому используем другой подход, основанный на развёртывании рекурентного соотношения: 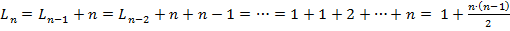
Дата добавления: 2015-10-13; просмотров: 171 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача о ханойской башне. | | | Доказательство неравенств. |