Алгоритм графического метода

1. Изобразите область допустимых решений. Если эта область – пустое множество, то задача недопустимая.

2. Постройте вектор . Его можно отложить от начала координат.

3. Постройте одну линию уровня, т.е. прямую, перпендикулярную вектору .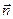

4. Линию уровня перемещайте по направлению вектора 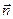в задаче на максимум, и против направления этого вектора в задаче на минимум до положения опорной прямой.

5. Если такого положения достигнуть невозможно, т.е. линия уровня уходит на бесконечность, то задача не ограничена: 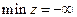или .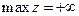

6. Если положение опорной прямой достигнуто, то угловая точка (или точки, если их несколько) области допустимых решений, которая лежит на опорной прямой, является точкой максимума или минимума, соответственно. Найдите координаты этой точки (или точек), значение целевой функции в этих точках и запишите ответ.

Пример. Решите задачу ,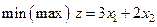

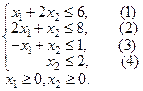
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат.

(1)				(2)				(3)
											–1

Прямая (4) проходит через точку параллельно оси .

Подставим точку (0;0) в ограничение (3), получим , что является истинным неравенством, поэтому стрелкой обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3).

Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений. Общей областью, разрешенной всеми ограничениями, является многоугольник ABCDEF.

Линию уровня можно построить по уравнению .

Строим вектор 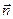из точки (0;0) в точку (3;2).

Точка Е – это крайняя точка области допустимых решений ABCDEF, через которую проходит линия уровня, двигаясь по направлению вектора 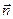. Поэтому Е – это точка максимума целевой функции.

Определим координаты точки Е из системы уравнений ограничений (1) и (2):

, .

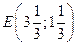Наибольшее значение: .

Если перемещать линию уровня в противоположном направлении, то получим точку минимума : .

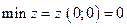Ответ: ; .

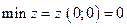Пример.

(1)				(2)				(4)
											–1

Прямая (3) проходит через точку параллельно оси .

Область допустимых решений – это незамкнутая область, ограниченная прямыми (2), (3), (4) и осью .

Строим вектор 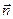из точки (0;0) в точку (1;–3). Для поиска минимума целевой функции передвигаем линию уровня против направления вектора 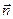. Поскольку в этом направлении область допустимых решений не ограничена, то невозможно в этом направлении найти крайнюю точку области допустимых решений.

Для поиска максимума будем передвигать линию уровня по направлению вектора 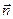до вершины А – крайней точки области допустимых решений в этом направлении. Определим координаты точки А из системы уравнений ограничений (2) и (4)

.

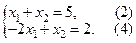
Максимальное значение целевой функции равно .

.

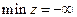Дата добавления: 2015-10-13