Каноническая форма задачи линейного программирования. Переход от общей формы к канонической

Постановка задачи линейного программирования

Пусть нужно найти экстремум линейной функции n переменных 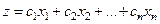, где 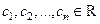, в области, заданной системой линейных уравнений и неравенств вида

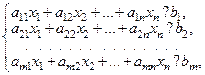
где 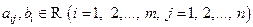, а знак «?» заменяет любой из знаков .

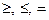Функция 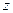называется целевой функцией.

Соотношения (равенства и неравенства) системы называются ограничениями задачи.

Множество решений системы ограничений называется допустимым множеством или областью допустимых решений.

Задача линейного программирования называется недопустимой, если область допустимых решений является пустым множеством.

Задача линейного программирования называется неограниченной, если целевая функция не ограничена сверху в задаче на максимум или не ограничена снизу в задаче на минимум. В этом случае пишут 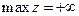или .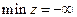

Каноническая форма задачи линейного программирования. Переход от общей формы к канонической

Задача линейного программирования задана в канонической форме, если она имеет вид:

,

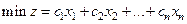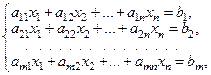
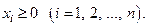
Т.е. задача линейного программирования задана в канонической форме, если выполняются три условия:

1) в задаче требуется найти минимум целевой функции;

2) все ограничения, входящие в систему – уравнения;

3) на все переменные наложены условия неотрицательности.

Если ввести обозначения 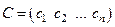, , 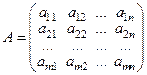, , 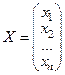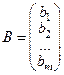то эту задачу можно записать в матричном виде

,

,

.

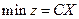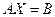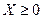Задачу линейного программирования общего вида можно привести к задаче в канонической форме, используя следующие преобразования.

1. Неравенство 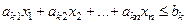приводится к уравнению добавлением в левую часть неравенства дополнительной неотрицательной переменной .

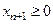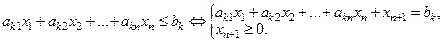
2. Неравенство 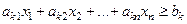приводится к уравнению вычитанием из левой части неравенства дополнительной неотрицательной переменной .

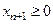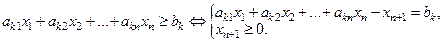
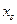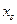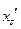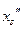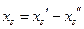3. Если для некоторой переменной, например, , нет требования неотрицательности, то представляют в виде разности двух неотрицательных переменных и : , где , .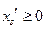

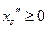4. От задачи на нахождение максимума функции 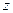переходим к задаче на нахождение минимума функции 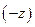. При этом .

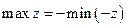Пример. Привести задачу к канонической форме

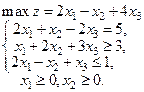
Решение. 1. Вместо 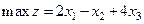будем искать .

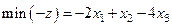2. Из левой части неравенства 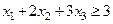вычтем 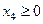, получим уравнение .

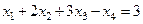3. К левой части неравенства 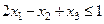прибавим 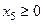, получим уравнение .

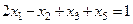4. На переменную 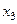не наложено условие неотрицательности. Заменим 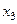разностью двух неотрицательных переменных , , .

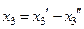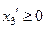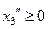Итак, получаем задачу в канонической форме

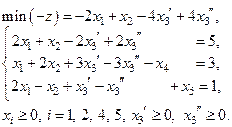
Дата добавления: 2015-10-13