Транспортная задача

Лекция №2

Напомним, что транспортная задача – частный случай задачи математического (линейного) программирования, суть которой заключается в следующем:

Имеется m поставщиков и n потребителей продукции. Известны cij - тарифы (стоимость) перевозок одной единицы продукции от i поставщика к j потребителю, известны объемы запасов у поставщиков ai и потребности каждого потребителя bj. Требуется составить план поставок продукции от поставщиков к потребителям так, чтобы суммарная стоимость перевозок была минимальной.

Обозначим через xij – объем перевозки груза от i поставщика к j потребителю. Тогда математическая постановка этой задачи будет иметь вид:

(1)

При этом должны соблюдаться условия:

- продукции должно быть вывезено не более произведенного количества:

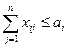, (2)

- платежеспособный спрос должен покрываться:

, (3)

(4)

Слово «транспортная» не означает, что эта задача может использоваться только для оптимизации перевозок, такое название она получила просто потому, что задача нахождения оптимальных по критерию минимизации суммарных транспортных затрат схем прикрепления потребителей к поставщикам исторически была первой в совокупности различных экономических проблем, решаемых с помощью моделей такого вида.

Задача (1 – 4) называется закрытой транспортной задачей, если . В этом случае ограничения (2) и (3) выполняются как равенства на всех допустимых планах. В противном случае, (т.е. когда 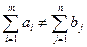) задача называется открытой. Многие алгоритмы решения транспортной задачи требует ее предварительного сведения к закрытой задаче путем введения дополнительных переменных (либо фиктивного поставщика, либо фиктивного потребителя с нулевыми тарифами).

Для решения транспортной задачи (1 – 4) используется более простой по сравнению с универсальным симплекс-методом метод потенциалов. Возможность его применения обусловлена сравнительной легкостью построения первоначального допустимого плана (например, методом северо-западного угла) и нахождения решения соответствующей ему системы уравнений двойственной задачи:

(6)

Из условия (6) следует, что для xij>0 должно выполняться условие:

(7)

а для xij=0 должно выполняться условие:

(8)

Одну из переменных двойственной задачи можно задать произвольно, остальные последовательно вычисляются из уравнений двойственной задачи).

Наличие нулевых невязок для небазисных переменных свидетельствует о множественности решений. К примеру, если х1 и х2 – оптимальные решения, то оптимальными будут и все решения, полученные по формуле aх1+(1-a)х2 при условии что 0‹a‹1). Оптимальное решение двойственной задачи также не является единственным: если все оценки («потенциалы пунктов производства и потребления») увеличить или уменьшить на одно и то же число, то новая совокупность оценок тоже будет решением двойственной задачи.

Среди всех решений двойственной задачи наибольшую ценность представляет «нормированное» решение – такое, в котором минимальная из всех переменных равна нулю, а все остальные, соответственно, неотрицательны. Только нормированные оценки имеют простую экономическую интерпретацию – они показывают, как изменится значение целевой функции при изменении на единицу соответствующего элемента вектора правых частей на единицу.

В рассмотренном выше примере полученная на последнем шаге система оценок случайно оказалась нормированной и изменение любого из параметров a и b на малую величину не приводит к смене базиса. Поэтому можно утверждать, например, что если бы значение a2 было равно 76, то при неизменности всех остальных параметров значение целевой функции на оптимальном плане уменьшилось бы на 1 единицу. Напротив, если бы значение b2 возросло на единицу, то суммарные транспортные затраты увеличились бы на 5 единиц.

Далеко не всегда пригодна универсальная постановка математической транспортной задачи, не требующая какой-либо дополнительной работы с информацией.

Дата добавления: 2015-10-13