Бесконечно большая

Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция 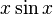, неограниченная с обеих сторон, не является бесконечно большой при .

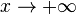Последовательность 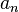называется бесконечно большой, если .

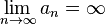Функция называется бесконечно большой в окрестности точки 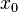, если .

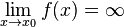Функция называется бесконечно большой на бесконечности, если 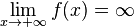либо .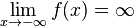

Как и в случае бесконечно малых, необходимо отметить, что ни одно отдельно взятое значение бесконечно большой величины не может быть названо как «бесконечно большое» – бесконечно большая величина — это функция, которая лишь в процессе своего изменения может стать больше произвольно взятого числа.

Примеры.

1. Последовательность 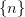является бесконечно большой, т.к. .

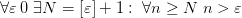2. Последовательность 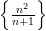является бесконечно большой, т.к. .

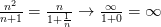3. 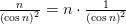– бесконечно большая, т.к. 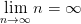, а 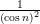– ограниченная, сохраняющая знак.

4.
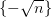
Выберем произвольное число 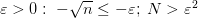. Получили: 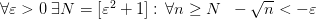, т.е. .

Дата добавления: 2015-10-13