Бесконечно малая

Бесконечно- малые и бесконечно-большие бесконечности

Выполнил студент гр. ПР – 282: Саврулин Егор Андреевич

Проверила: Ядринникова Светлана Леонидовна

2015 г.

Бесконечно-малые бесконечности

Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.

Бесконечно малая

Последовательность 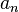называется бесконечно малой, если . Например, последовательность чисел — бесконечно малая.

Функция называется бесконечно малой в окрестности точки 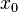, если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то , .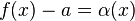

Подчеркнём, что бесконечно малую величину следует понимать как переменную величину (функцию), которая лишь в процессе своего изменения [при стремлении к (из )] делается меньше произвольного числа (). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе [абсолютном значении] не имеет смысла говорить, что оно бесконечно малое.

Дата добавления: 2015-10-13