Методы решения нелинейных конечных уравнений

Необходимость решения нелинейных конечных уравнений в электромеханике возникает в задачах расчета нелинейных электрических кругов, проектирования разных видов электрических машин и аппаратов, и тому подобное.

Задачу определения корня нелинейного конечного уравнения

(1.1)

с использованием ЭВМ обычно решают численными итерационными методами, суть которых заключается в том, что, задавшись нулевым приближением X₀ корня, определяют его первое приближение X₁, по значению X₁ определяют второе приближение X₂ и так далее Если разница с ростом j становится все меньшей, то говорят, что итерационный процесс совпадает. Его можно прекратить, когда выполнится неравенство

,(1.2)

где - заранее задано малое число (погрешность). Для применения рассмотренных ниже методов следует сначала тем или иным способом найти интервал [а;b], в котором находится отыскиваемый корень уравнения (1.1). Если удовлетворяется условие

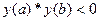, (1.3)

то есть функция y=y(x) на концах этого интервала имеет разные знаки, то это значит, что интервал содержит в себе один корень. Если на интервале удовлетворяется условие

(1.4)

то есть первая производная функции y=y(x) не изменяет свой знак (функция y=y(x) монотонна), то это значит, что на интервале [а;b] расположен только один корень.

Дата добавления: 2015-10-13