Основные теоретические положения

Нелинейные уравнения в електротехнике:

Нелинейные алгебраичные уравнения чаще всего используются в электротехнике при расчетах нелинейных кругов.

Нелинейными кругами называют такие круги, которые содержат в себе хотя бы один нелинейный элемент. Рассмотрим круги постоянного тока. В этих кругах присутствуют нелинийни резисторы. Известно, что у резистора зависимость между током и напряжением описывается законом Ома: . Эта зависимость может применяться лишь тогда, когда резистор имеет одно и то же сопротивление независимо от значений напряжений и токов.

Но часто бывают так, что сопротивление резистора изменяется в зависимости от тока, который действует через этот резистор. Например, при действии тока через любой проводник этот проводник будет нагреваться, из-за чего его сопротивление должно увеличиваться. То есть при увеличении тока сопротивление любого проводника увеличивается. Это значит, что в природе вообще нет линейных сопротивлений. Линейными можем считать лишь так называемые идеальные элементы. Расчет кругов с нелинейными элементами значительно более сложен, чем линейных кругов. Именно здесь применяются ЭВМ.

Рассмотрим расчет нелинейных кругов с помощью метода эквивалентного генератора. При применении этого метода вся линейная часть схемы заменяется эквивалентным источником напряжения и линейным сопротивлением – так называемым эквивалентным генератором. Схема эквивалентного генератора с подключённым к нему нелинейным сопротивлением приведенна на рис. 1.

Re

Рис.1. Еквівалентний генератор

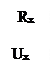Рядом (рис. 2) приведены вольт-амперные характеристики нелинейного сопротивления (Rx) и эквивалентного генератора. Характеристика эквивалентного генератора – это прямая, которая проходит через точку Eе по оси ординат (напряжение) и Ee/re на оси абсцисс (ток). Из этого графика видно, что ток в нелинейном резисторе и напряжение на нем можно определить, если будем знать координаты точки пересечения этих двух вольт-амперных характеристик. Найдем эти координаты. Будем считать, что зависимость 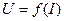, то есть вольт-амперная характеристика нелинейного сопротивления, известная. На основании второго закона Кирхгофа можно доказать, что вольт-амперная характеристика эквивалентного генератора – это есть зависимость 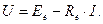Для точки пересечения можно записать:

(1)

Это значит, что ток Ix может быть найден как решение этого нелинейного уравнения (1).

Задание:

Согласно варианту составить программы для решения нелинейного уравнения (1). Вычисление значения функций 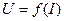выполнить с помощью подпрограммы – функции.

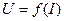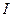Общий вид нелинейных уравнений задается полиномом пятой степени: , где под имеется в виду . Значение коэффициентов 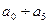приведено в таблице вариантов.

Дата добавления: 2015-10-13