Кривые линии

Отчет о самоподготовке по ИиКГ

Студента МТУСИ

Группы БРТ 1101

Разоренова Димитрия

Проверил: Евстратов П.И.

Кривые линии

Кривая – это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по разному. В начертательной геометрии кривую рассматривают как:

· траекторию, описанную движущейся точкой,

· проекцию другой кривой,

· линию пересечения двух поверхностей.

Кривые бывают пространственные и плоские. Кривая называется плоской, если все ее точки принадлежат некоторой плоскости, в противном случае она называется пространственной.

На ортогональном чертеже кривые линии задают проекциями. При этом, в отличие от задания прямой, необходимо задать по крайне мере проекции одной точки, принадлежащей кривой.

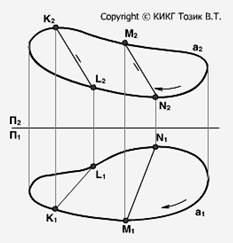
На ортогональном чертеже заданы проекции кривой а.

Если бы не были бы заданы проекции точки K, мы не могли бы построить горизонтальную проекцию M1 точки M по имеющейся фронтальной проекции M2.

По чертежу кривой в общем случае можно без дополнительных построений определить плоская она или пространственная.

На чертеже задана пространственная кривая а, т. к. прямаяK2L2 параллельна прямой M2N2, a K1L1 не параллельна M1N1.

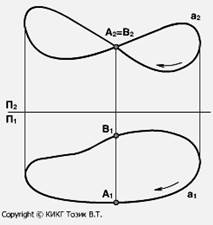
На чертеже явно задана пространственная кривая, имеющая конкурирующие точки А и В: (А2 = В2).

Форма технических объектов нередко содержит плавные переходы. На чертежах переходы изображаются сопряжением окружностей и прямых линий.

Сопряжение – плавный переход с окружности на прямую. Для построения сопряжений необходимо понять логику построения. Основой сопряжений евляются положение о геометрических местах точек. В таблице Геометрические основы сопряжений мы можем наблюдать геомметрические места точек равноудалённых от

а) Концов отрезка,

б) Прямой,

в) Окружности

г) Сторон угла,

д) Точки.

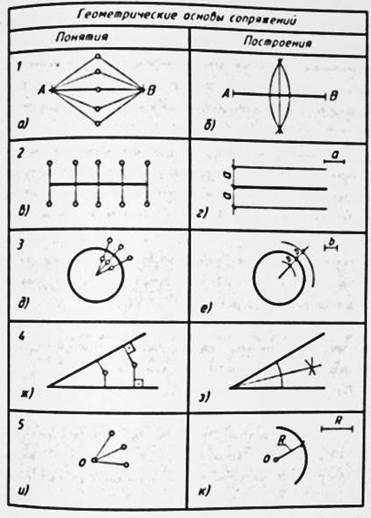И так мы видим, что ГМТ равноудалённых от концов отрезка, является прямая, Равноудалённых от прямой – две прямые; от окружности – две окружности; От сторон угл – его биссектриса и от точки – окружность.

Дата добавления: 2015-10-13