Определим операторным методом закон изменения переходного процесса при замыкании ключа в случае постоянной ЭДС источника.

Определим независимые начальные условия (ННУ):

Для нахождения напряжения на емкости воспользуемся методом узловых потенциалов. Запишем систему уравнений по методу узловых потенциалов.

Решив систему уравнений найдем значение узловых потенциалов в операторном виде:

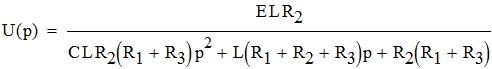
Определим закон изменения переходного процесса в операторном виде:

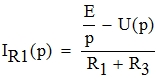
Упростим выражение для закона изменения переходного процесса в операторном виде:

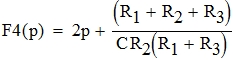
Решая уравнение F3(p)=0 приходим к квадратному p²+ap+b=0, где:

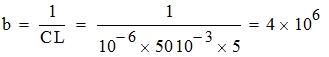
По теореме разложения найдем оригинал операторного закона изменения переходного процесса:

Рис.2 График переходного процесса при постоянном напряжении источника.

Как видно из графиков (Рис.1 и Рис.2), данные полученные операторным и классическим методом полностью идентичны, что подтверждает правильность произведенных расчетов.

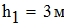
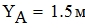
Определим частичные емкости между каждым проводом и проводящей поверхностью:

Первая группа формул Максвелла для системы из 3-х проводов имеет вид:

где потенциальные коэффициенты α_ij определяются формулой:

коэффициенты b_ij и a_ij определяют расстояние от i-го провода до j-го зеркального изображения и расстояние от i-го провода до j-го провода соответственно.

Потенциальные коэффициенты α_ii определяются формулой:

Коэффициенты h_i и r_i определяют высоту подвеса от i-го провода и расстояние от i-го радиус до i-го провода.

Определим собственные потенциальные коэффициенты α_ii:

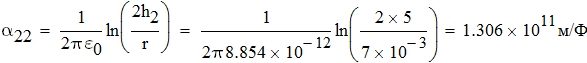
Определим взаимные потенциальные коэффициенты α_ij:

Матрица потенциальных коэффициентов α_ij имеет вид:

Вторая группа формул Максвелла для системы из 3-х проводов имеет вид:

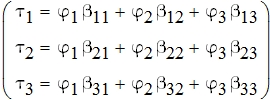
где емкостные коэффициенты β_ij определяются формулой:

Коэффициенты Δ_ij и Δ вычисляются как минор и определитель матрицы потенциальных коэффициентов соответственно. Вычислим миноры и определитель матрицы потенциальных коэффициентов

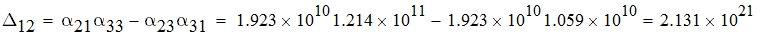
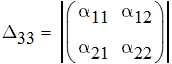
В силу симметричности матрицы потенциальных коэффициентов:

Определим емкостные коэффициенты:

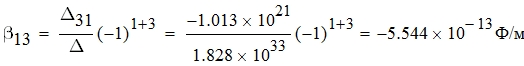
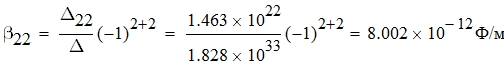
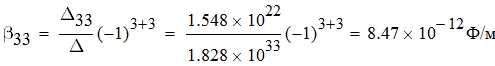
В силу симметричности матрицы потенциальных коэффициентов:

Матрица емкостных коэффициентов β_ij имеет вид:

Третья группа формул Максвелла для системы из 3-х проводов имеет вид:

где собственные частичные емкости C_ii определяются формулой:

где взаимные частичные емкости C_ij определяются формулой:

Определим взаимные частичные емкости между проводами C_ij используя ранее полученные значения емкостных коэффициентов β_ij:

Определим собственные частичные емкости между проводами и проводящей поверхностью C_ii используя ранее полученные значения емкостных коэффициентов β_ij:

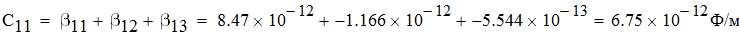
Дата добавления: 2015-10-13