Определим классическим методом закон изменения переходного процесса при замыкании ключа в случае постоянной ЭДС источника.

Рассчитаем параметры схемы в момент коммутации.

Определим независимые начальные условия (ННУ):

Определим зависимые начальные условия (ЗНУ), используя метод суперпозиций.

Чтобы определить закон изменения переходного процесса используем искусственный прием - для послекоммутационной схемы разорвем произвольно выбранную ветвь и относительно разрыва найдем входное сопротивление Z_вх(p) (полагая Z_ист=0), где p=jw. Решив уравнение Z_вх(p)=0 найдем его корни, которые определят закон изменения переходного процесса.

Решая уравнение Zвх=0 приходим к квадратному p²+ap+b=0, где:

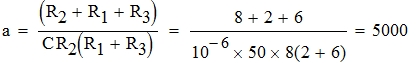
Т.к. корни вещественные и отрицательные, то переходный процесс будет апериодическим и затухающим вида A₁e^p1t+A₂e^p2t, где:

p₁, p₂ - коэффициенты затухания,

τ - постоянная времени цепи.

Определим принужденную составляющую.

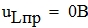
Закон изменения напряжения на емкости и тока через индуктивность будет иметь вид:

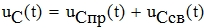
Найдем коэффициенты A₁,A₂, для этого продифференцируем выражение для напряжения на емкости.

Положим t=0 и найдем A₁, A₂.

Отсюда находим A₁ и A₂:

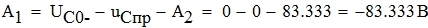
Найдем коэффициенты B₁ и B₂, для этого продифференцируем выражение для тока через индуктивность.

Положим t=0 и найдем B₁ и B₂.

Отсюда находим B₁ и B₂:

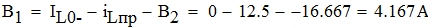
Найдем закон изменения переходного процесса.

Введем новые коэфициенты C₁ и C₂:

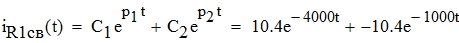
Рис.1 График переходного процесса (с разложением на составляющие) при постоянном напряжении источника на интервале 0...3τ..

Дата добавления: 2015-10-13