
|
Читайте также: |
Типовой расчет
Приложения определенных интегралов.
Теоретические вопросы.
1. Задачи, приводящие к понятию определенного интеграла. Интегральная сумма. Определение интеграла. Теорема существования (без доказательства). Геометрический смысл определенного интеграла.
2. Основные свойства определенного интеграла.
3. Теорема о среднем значении определенного интеграла и ее геометрический смысл.
4. Производная определенного интеграла по переменному верхнему пределу.
5. Формула Ньютона – Лейбница.
6. Замена переменной и интегрирование по частям в определенном интеграле.
7. Приближенное вычисление определенных интегралов.
8. Приложения определенных интегралов в геометрии и механике (вычисление площадей фигур, длин дуг, объемов тел, статических моментов, координат центра тяжести, моментов инерции и др.)
9. Несобственные интегралы с бесконечными пределами и от разрывных функций.
Индивидуальные задания к типовому расчету.
Задание 1. Вычислить определенные интегралы:
1.1. а)  ; б)
; б) 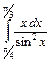 .
.
1.2. а)  ; б)
; б) 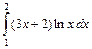 .
.
1.3. а) 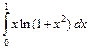 ; б)
; б)  .
.
1.4. а) 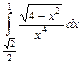 ; б)
; б) 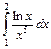 .
.
1.5. а) 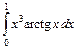 ; б)
; б)  .
.
1.6. а)  ; б)
; б)  .
.
1.7. а)  ; б)
; б)  .
.
1.8. а)  ; б)
; б)  .
.
1.9. а)  ; б)
; б) 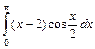 .
.
1.10. а)  ; б)
; б)  .
.
1.11. а)  ; б)
; б) 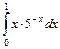 .
.
1.12. а) 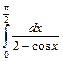 ; б)
; б)  .
.
1.13. а) 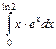 ; б)
; б) 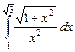 .
.
1.14. а)  ; б)
; б) 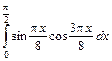 .
.
1.15. а) 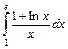 ; б)
; б)  .
.
1.16. а)  ; б)
; б)  .
.
1.17. а) 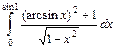 ; б)
; б)  .
.
1.18. а) 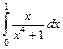 ; б)
; б)  .
.
1.19. а)  ; б)
; б)  .
.
1.20. а) 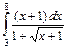 ; б)
; б) 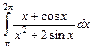 .
.
1.21. а) 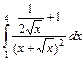 ; б)
; б) 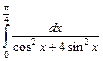 .
.
1.22. а)  ; б)
; б)  .
.
1.23. а)  ; б)
; б) 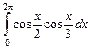 .
.
1.24. а)  ; б)
; б)  .
.
1.25. а) 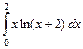 ; б)
; б)  .
.
1.26. а)  ; б)
; б) 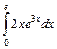 .
.
1.27. а) 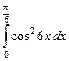 ; б)
; б) 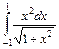 .
.
1.28. а)  ; б)
; б)  .
.
1.29. а)  ; б)
; б)  .
.
1.30. а) 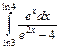 ; б)
; б) 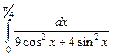 .
.
Задание 2. Вычислить несобственные интегралы, если они сходятся.
2.1. 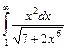 2.2.
2.2. 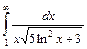 2.3.
2.3. 
2.4.  2.5.
2.5.  2.6.
2.6. 
2.7. 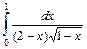 2.8.
2.8. 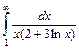 2.9.
2.9. 
2.10.  2.11.
2.11.  2.12.
2.12. 
2.13.  2.14.
2.14.  2.15.
2.15. 
2.16.  2.17.
2.17. 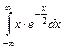 2.18.
2.18. 
2.19.  2.20.
2.20.  2.21.
2.21. 
2.22. 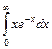 2.23.
2.23. 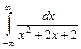 2.24.
2.24. 
2.25. 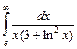 2.26.
2.26.  2.27.
2.27. 
2.28.  2.29.
2.29.  2.30.
2.30. 
Задание 3. Вычислить площади фигур, ограниченных линиями:
3.1. а) 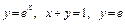 ;
;
б) 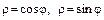 ;
;
в)  ,
,  .
.
3.2. а)  ;
;
б)  (большей части);
(большей части);
в)  ,
,  .
.
3.3. а)  ;
;
б)  ;
;
в)  ,
,  .
.
3.4. а)  ;
;
б)  ;
;
в)  ,
,  .
.
3.5. а)  ;
;
б)  ;
;
в) 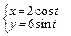 ,
,  .
.
3.6. а)  ;
;
б) 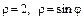 ;
;
в)  ,
,  .
.
3.7. а) 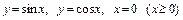 ;
;
б)  (большей из фигур);
(большей из фигур);
в)  ,
, 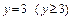 .
.
3.8. а)  ;
;
б) 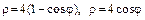 ;
;
в)  ,
,  .
.
3.9. а) 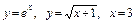 ;
;
б)  (большей части);
(большей части);
в) 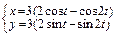 ,
,  .
.
3.10. а)  ;
;
б) 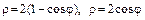 ;
;
в)  ,
,  .
.
3.11. а) 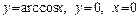 ;
;
б) 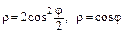 ;
;
в)  ,
, 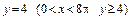 .
.
3.12. а) 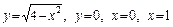 ;
;
б)  ;
;
в) 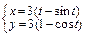 ,
,  .
.
3.13. а)  ;
;
б) 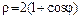 (части, лежащей во II четверти);
(части, лежащей во II четверти);
в)  ,
,  .
.
3.14. а) 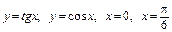 ;
;
б)  ;
;
в) 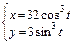 ,
, 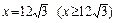 .
.
3.15. а)  ;
;
б)  ;
;
в) 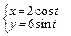 ,
, 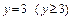 .
.
3.16. а)  ;
;
б)  ;
;
в) 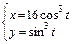 ,
, 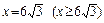 .
.
3.17. а) 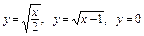 ;
;
б) 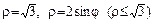 ;
;
в)  ,
, 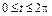 .
.
3.18. а)  ;
;
б)  ;
;
в)  ,
, 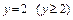 .
.
3.19. а)  ;
;
б)  ;
;
в) 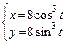 ,
,  .
.
3.20. а) 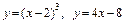 ;
;
б) 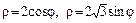 ;
;
в)  ,
,  .
.
3.21. а)  ;
;
б)  ;
;
в)  ,
,  .
.
3.22. а)  ;
;
б) 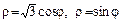 ;
;
в) 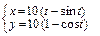 ,
,  .
.
3.23. а)  ;
;
б)  ;
;
в)  ,
,  .
.
3.24. а) 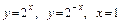 ;
;
б) 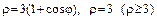 ;
;
в)  .
.
3.25. а)  ;
;
б) 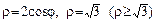 ;
;
в)  ,
, 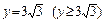 .
.
3.26. а)  ;
;
б)  ;
;
в)  ,
,  .
.
3.27. а)  ;
;
б)  ;
;
в)  ,
, 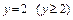 .
.
3.28. а)  ;
;
б)  ;
;
в) 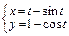 , одной аркой и прямой
, одной аркой и прямой  .
.
3.29. а)  и касательными к ней в точках
и касательными к ней в точках 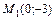 и
и
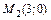 ;
;
б)  , лежащую вне круга
, лежащую вне круга  ;
;
в) 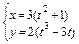 (вычислить площадь петли).
(вычислить площадь петли).
3.30. а)  , касательной к ней в точке
, касательной к ней в точке 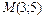 и осью
и осью
ординат;
б)  и координатными осями;
и координатными осями;
в)  , содержащуюся внутри петли.
, содержащуюся внутри петли.
Задание 4. Вычислить длину дуги плоской кривой.
4.1. а)  ;
;
б)  ,
,  ;
;
в)  .
.
4.2. а)  ;
;
б) 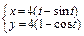 (одной арки);
(одной арки);
в)  (первого витка).
(первого витка).
4.3. а)  ;
;
б) 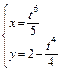 , между точками пересечения с координатными
, между точками пересечения с координатными
осями;
в) 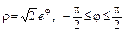 .
.
4.4. а) 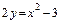 , между точками пересечения с осью
, между точками пересечения с осью  .
.
б)  ,
, 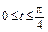 .
.
в)  .
.
4.5. а)  ;
;
б)  ,
, 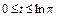 ;
;
в)  .
.
4.6. а)  ;
;
б)  (длину петли кривой);
(длину петли кривой);
в)  .
.
4.7. а) 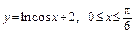 ;
;
б) 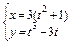 (длину петли кривой);
(длину петли кривой);
в)  .
.
4.8. а) 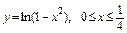 ;
;
б)  ,
,  ;
;
в)  .
.
4.9. а)  ;
;
б)  ,
,  ;
;
в) 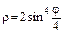 .
.
4.10. а)  ;
;
б) 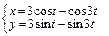 ,
,  ;
;
в)  .
.
4.11. а) 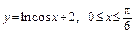 ;
;
б) 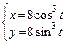 ,
,  ;
;
в)  .
.
4.12. а)  ;
;
б)  ,
,  ;
;
в) 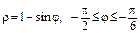 .
.
4.13. а)  ;
;
б)  ,
,  ;
;
в)  .
.
4.14. а) 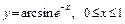 ;
;
б) 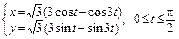 ;
;
в)  .
.
4.15. а)  ;
;
б)  ;
;
в) 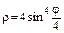 .
.
4.16. а)  ;
;
б) 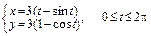 ;
;
в)  .
.
4.17. а)  ;
;
б) петли  ;
;
в)  .
.
4.18. а)  ;
;
б)  ,
,  ;
;
в)  .
.
4.19. а)  , между точками пересечения с осью
, между точками пересечения с осью  ;
;
б) петли 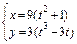 ;
;
в) 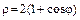 .
.
4.20. а)  ;
;
б)  ;
;
в)  .
.
4.21. а) 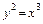 от
от  до
до  ;
;
б)  ;
;
в)  , отсекаемой от параболы вертикальной прямой,
, отсекаемой от параболы вертикальной прямой,
проходящей через полюс.
4.22. а)  ;
;
б)  ;
;
в)  .
.
4.23. а)  ;
;
б) петли 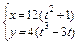 ;
;
в)  .
.
4.24. а) 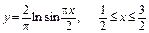 ;
;
б) 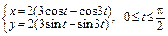 ;
;
в) 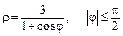 .
.
4.25. а)  ;
;
б)  ;
;
в)  .
.
4.26. а)  , отсекаемой осью
, отсекаемой осью  ;
;
б) 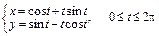 ;
;
в)  .
.
4.27. а)  , отсекаемой прямой
, отсекаемой прямой  ;
;
б)  ;
;
в)  .
.
4.28. а) периметр фигуры, ограниченной линиями 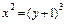 и
и
 ;
;
б)  ;
;
в) 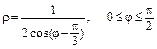 .
.
4.29. а) 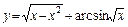 ;
;
б)  ,
,  ;
;
в)  .
.
4.30. а) периметр фигуры, ограниченной линиями  и
и  ;
;
б) 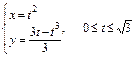 ;
;
в)  .
.
Задание 5. Найти объем тела, полученного при вращении фигуры, ограниченной линиями:
5.1.  вокруг оси
вокруг оси  .
.
5.2. 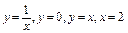 вокруг оси
вокруг оси  .
.
5.3.  вокруг оси
вокруг оси  .
.
5.4. 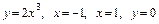 вокруг оси
вокруг оси 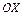 .
.
5.5. 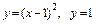 вокруг оси
вокруг оси  .
.
5.6.  вокруг оси
вокруг оси  .
.
5.7.  вокруг оси
вокруг оси  .
.
5.8. 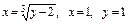 вокруг оси
вокруг оси  .
.
5.9.  вокруг оси
вокруг оси  .
.
5.10.  вокруг оси
вокруг оси  .
.
5.11.  вокруг оси
вокруг оси  .
.
5.12.  вокруг оси
вокруг оси  .
.
5.13. 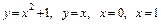 вокруг оси
вокруг оси  .
.
5.14. 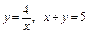 вокруг оси
вокруг оси  .
.
5.15. 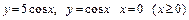 вокруг оси
вокруг оси  .
.
5.16.  вокруг оси
вокруг оси  .
.
5.17.  вокруг оси
вокруг оси  .
.
5.18.  вокруг оси
вокруг оси  .
.
5.19.  вокруг оси
вокруг оси  .
.
5.20. 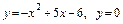 вокруг оси
вокруг оси  .
.
5.21.  вокруг оси
вокруг оси  .
.
5.22. 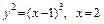 вокруг оси
вокруг оси  .
.
5.23.  вокруг оси
вокруг оси  .
.
5.24.  вокруг оси
вокруг оси  .
.
5.25.  вокруг оси
вокруг оси  .
.
5.26. 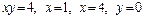 вокруг оси
вокруг оси  .
.
5.27.  вокруг оси
вокруг оси  .
.
5.28. 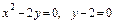 вокруг оси
вокруг оси  .
.
5.29.  вокруг оси
вокруг оси  .
.
5.30.  вокруг оси
вокруг оси  .
.
Дата добавления: 2015-10-13; просмотров: 142 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Часть 4 из 4: Нудизм вне дома | | | Конопля |