Условие задания.

Для функций нагрузок и функций прогибов требуется:

1. установить граничные условия, которым удовлетворяет функция прогибов ;

2. проверить, удовлетворяет ли функция уравнению Софи-Жермен , и, если это не так, то использовать уравнение Бубнова-Галёркина:

Из этих уравнений определить постоянную С; записать выражение максимального прогиба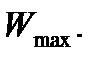

3. по формулам для составить их выражения;

4. в опасных сечениях пластинки построить эпюры 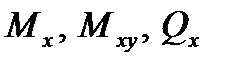в сечении, перпендикулярном оси x и эпюры 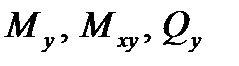в сечении перпендикулярном оси y;

5. в этих же сечениях пластинки построить эпюры напряжений по её толщине;

6. исходя из энергетической теории прочности, подобрать толщину пластинки h.

Числовые данные:

a

0 x

C

b

A B

y

Рис. 1. Расчётная схема пластинки.

РЕШЕНИЕ:

1. Установим, каким граничным условиям удовлетворяет функция прогибов:

для заданной пластинки.

Грань АB: y=b;.

(прогиб);

(угол поворота);

(изгибающий момент);

Вывод: шарнирно опертый край

Грань ВС: x=a;

(прогиб);

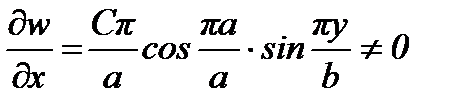(угол поворота).

(изгибающий момент);

Вывод: шарнирно опертый край

Грань АB: y=0;.

(прогиб);

(угол поворота);

(изгибающий момент);

Вывод: шарнирно опертый край

Грань ОА: x=0;

(прогиб);

(угол поворота).

(изгибающий момент);

Вывод: шарнирно опертый край

О C

у

b = 2,4 м

А B

х a = 1,6 м

Рис. 2. Схема закрепления пластинки.

2. Воспользуемся уравнением Софи Жермен. Для этого вычислим производные:

Подставим значения производных и в уравнение Софи Жермен.

Видим что оно не удовлетворяется т.к слева и справа разные зависимости.

Применим метод Бубнова –Галёркина:

Выполняя решение на ЭВМ (см. распечатку), получим:

Анализ функции прогибов свидетельствует, что максимальный прогиб пластинка испытывает в точке с координатами x =а/2=0,8 м; y =b/2=1,2 м. Итак:

2. Составим выражения для . Для этого вычислим необходимые производные:

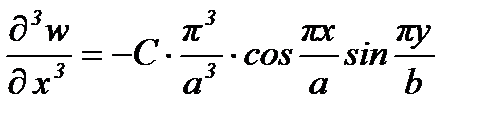
Тогда с учётом выражения для С, получим:

3. Построим эпюру в сечении, где x=0,8 и эпюру в сечении где y=1,2.

Построение выполняем по данным полученным машинным расчетом.

Рис. 3.

4. Построим эпюры напряжений

при z = h/2

при z = h/2

5. По этим данным строим эпюры:

6. Исходя из энергетической теории прочности, подберём толщину пластинки h. Условие прочности имеет вид:

Главные напряжения определяются как корни кубического уравнения:

где – инварианты напряжённого состояния.

При изгибе пластинки напряжением пренебрегают. Кроме того, в нашем случае 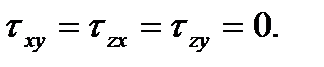Поэтому инварианты имеют вид:

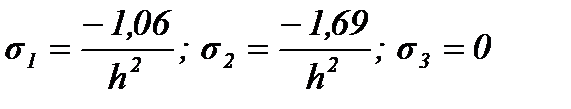
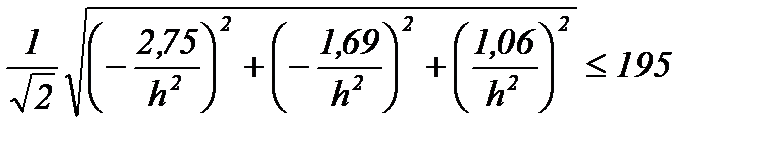
Окончательно принимаем пластинку, толщиной равной 12 см.

P306

Вариант 18

Размеpы пластинки а_х = 1.60 b_y = 2.40 Qo = 3.10 Ma

Значение коэффициента С = -0.066/D

Значения моментов Mx [10^3 кН*м/м]

.000.000.000.000.000.000.000.000.000.000.000

.000 -.027 -.051 -.070 -.083 -.087 -.083 -.070 -.051 -.027.000

.000 -.051 -.097 -.134 -.157 -.165 -.157 -.134 -.097 -.051.000

.000 -.070 -.134 -.184 -.216 -.228 -.216 -.184 -.134 -.070.000

.000 -.083 -.157 -.216 -.254 -.267 -.254 -.216 -.157 -.083.000

.000 -.087 -.165 -.228 -.267 -.281 -.267 -.228 -.165 -.087.000

.000 -.083 -.157 -.216 -.254 -.267 -.254 -.216 -.157 -.083.000

.000 -.070 -.134 -.184 -.216 -.228 -.216 -.184 -.134 -.070.000

.000 -.051 -.097 -.134 -.157 -.165 -.157 -.134 -.097 -.051.000

.000 -.027 -.051 -.070 -.083 -.087 -.083 -.070 -.051 -.027.000

.000.000.000.000.000.000.000.000.000.000.000

Значения моментов Mу [10^3 кН*м/м]

.000.000.000.000.000.000.000.000.000.000.000

.000 -.017 -.032 -.044 -.052 -.054 -.052 -.044 -.032 -.017.000

.000 -.032 -.061 -.084 -.098 -.103 -.098 -.084 -.061 -.032.000

.000 -.044 -.084 -.115 -.135 -.142 -.135 -.115 -.084 -.044.000

.000 -.052 -.098 -.135 -.159 -.167 -.159 -.135 -.098 -.052.000

.000 -.054 -.103 -.142 -.167 -.176 -.167 -.142 -.103 -.054.000

.000 -.052 -.098 -.135 -.159 -.167 -.159 -.135 -.098 -.052.000

.000 -.044 -.084 -.115 -.135 -.142 -.135 -.115 -.084 -.044.000

.000 -.032 -.061 -.084 -.098 -.103 -.098 -.084 -.061 -.032.000

.000 -.017 -.032 -.044 -.052 -.054 -.052 -.044 -.032 -.017.000

.000.000.000.000.000.000.000.000.000.000.000

Значения моментов Mxy=Myx [10^3 кН*м/м]

.127.120.102.074.039.000 -.039 -.074 -.102 -.120 -.127

.120.114.097.071.037.000 -.037 -.071 -.097 -.114 -.120

.102.097.083.060.032.000 -.032 -.060 -.083 -.097 -.102

.074.071.060.044.023.000 -.023 -.044 -.060 -.071 -.074

.039.037.032.023.012.000 -.012 -.023 -.032 -.037 -.039

.000.000.000.000.000.000.000.000.000.000.000

-.039 -.037 -.032 -.023 -.012.000.012.023.032.037.039

-.074 -.071 -.060 -.044 -.023.000.023.044.060.071.074

-.102 -.097 -.083 -.060 -.032.000.032.060.083.097.102

-.120 -.114 -.097 -.071 -.037.000.037.071.097.114.120

-.127 -.120 -.102 -.074 -.039.000.039.074.102.120.127

Значения попеpечных сил Qx [10^3 кН/м]

.000.000.000.000.000.000.000.000.000.000.000

-.223 -.211 -.179 -.130 -.069.000.069.130.179.211.223

-.424 -.401 -.341 -.248 -.130.000.130.248.341.401.424

-.584 -.552 -.470 -.341 -.179.000.179.341.470.552.584

-.687 -.649 -.552 -.401 -.211.000.211.401.552.649.687

-.722 -.683 -.581 -.422 -.222.000.222.422.581.683.722

-.687 -.649 -.552 -.401 -.211.000.211.401.552.649.687

-.584 -.552 -.470 -.341 -.179.000.179.341.470.552.584

-.424 -.401 -.341 -.248 -.130.000.130.248.341.401.424

-.223 -.211 -.179 -.130 -.069.000.069.130.179.211.223

.000.000.000.000.000.000.000.000.000.000.000

Значения попеpечных сил Qy [10^3 кН/м]]

.000 -.148 -.282 -.388 -.456 -.480 -.456 -.388 -.282 -.148.000

.000 -.141 -.268 -.368 -.433 -.455 -.433 -.368 -.268 -.141.000

.000 -.120 -.228 -.313 -.368 -.387 -.368 -.313 -.228 -.120.000

.000 -.087 -.165 -.228 -.268 -.281 -.268 -.228 -.165 -.087.000

.000 -.046 -.087 -.120 -.141 -.148 -.141 -.120 -.087 -.046.000

.000.000.000.000.000.000.000.000.000.000.000

.000.046.087.120.141.148.141.120.087.046.000

.000.087.165.228.268.281.268.228.165.087.000

.000.120.228.313.368.387.368.313.228.120.000

.000.141.268.368.433.455.433.368.268.141.000

.000.148.282.388.456.480.456.388.282.148.000

Дата добавления: 2015-10-13