Средние величины в статистике, их значение и условия применения.

Чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, прибегают к расчёту средних величин. Средние величины – показатели, которые выражают типичные размеры и черты и дают обобщающую количественную характеристику по качественно однородным общественным явлениям. Средняя характеризует признак совокупности в расчёте на 1 единицу совокупности. Любая единица объединяет в себе:

• типичные черты (значение средней)
• индивидуальные черты (то, насколько эта единица отличается от средней)

Чаще всего средние величины рассчитывают по сгруппированным данным. В эк. практике используется широкий круг показателей, вычисленных в виде средних величин.

Средний показатель должен определяться для совокупностей, состоящих из качественно однородных единиц. Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления, фальсьфицировать его или будут бессмысленными.

Виды средних величин:

• средняя арифметическая
• средняя гармоническая
• средняя хронологическая
• средняя структурная
• вариация

26. Методы расчётов средних величин в зависимости от характера исходных данных.

Средние величины в статистике:

• средняя арифметическая – в зависимости от характера исходных данных бывает:

– невзвешенная (если данные нельзя сгруппировать)

– взвешенная (если данные можно сгруппировать)

• средняя гармоническая – это обратная величина среднеарифметической:

– невзвешенная

– взвешенная

• средняя хронологическая (как правило, применяется в торговле и ресторанных хозяйствах для исчисления среднего товарного запаса):

• средняя структурная – это мода и медиана.

Мода (Мо) – это наиболее часто повторяющаяся величина в статистическом ряду распределения. Для интервального ряда распределения мода высчитывается по специальной формуле:

Mo = Xm_o + Im_o x

Медиана (Ме) – это серединное значение, которое делит ранжированный ряд распределения пополам. Рассчитывается только для ранжированного ряда распределния.

• вариация – колеблемость изучаемого признака:

– размах (R) R = xmax - xmin

– среднее квадратическое отклонение (σ):

взвешенное

невзвешенное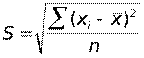

– коэффициент вариации (V)

– дисперсия (σ 2):

взвешенная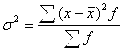

невзвешенная

Дата добавления: 2015-09-07