ЧАСТЬ 1. Контрольных измерительных материалов для проведения регионального экзамена по

Контрольных измерительных материалов для проведения регионального экзамена по МАТЕМАТИКЕ

В 8-х классах общеобразовательных учреждений

Оренбургской области в 2012-2013 учебном году

Пояснения к демонстрационному варианту

Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику экзамена по математике в 8 классе и широкой общественности составить представление о структуре и содержании будущих вариантов экзаменационной работы, о форме предъявления материала и уровне сложности заданий. Критерии оценивания экзаменационной работы позволят составить представление о требованиях к полноте и правильности ответов.

Эти сведения дают возможность учащимся выработать стратегию подготовки к сдаче регионального экзамена по математике.

Инструкция по выполнению работы

На выполнение экзаменационной работы отводится 90 минут. Работа состоит из двух частей. Первая часть содержит 9 заданий базового уровня сложности, вторая часть – 3 задания повышенного уровня сложности.

Решения всех задач экзаменационной работы (первой и второй частей) и ответы к ним записываются на отдельных листах.

Формулировки заданий не переписываются, рисунки не перечерчиваются. После решения задачи записывается ответ, при записи которого учитывается следующее:

ü в заданиях с выбором ответа указывается номер верного ответа;

ü в заданиях с кратким ответом указывается число (целое число или десятичная дробь), получившееся в результате решения;

ü в задании на соотнесение указывается последовательность цифр из таблицы ответов без использования букв, пробелов и других символов (неправильно: А-2, Б-1, В-3; правильно: 213).

Все необходимые вычисления, преобразования производятся в черновике. Черновики не проверяются и не учитываются при выставлении отметки.

Правильный ответ в зависимости от сложности каждого задания оценивается одним или несколькими баллами. Баллы, полученные вами за все выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать как можно больше баллов.

Желаем успеха!

ЧАСТЬ 1

	Моторная лодка движется по течению реки со скоростью 21 км/ч, а против течения – со скоростью 15 км/ч. Какую часть от собственной скорости лодки составляет скорость течения реки?
1) 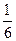;	2) ;	3) 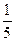;	4) .

В таблице приведена приблизительная численность учащихся и педагогов общеобразовательных школ и интернатов России по городам (тыс. чел. к началу учебного года).  

	1940/41	1950/51	1960/61	1970/71	1980/81	1990/91	2000/01	2005/06	2006/07
Учащиеся
Педагоги

На сколько процентов уменьшилось число школьников к сентябрю 1980 года по сравнению с сентябрем 1970 года? Ответ: _______________.

 

Каждому выражению из левого столбца поставьте в соответствие его значение из правого столбца:

А) ; Б) ; В) ;

1) 3; 2) 1; 3) 0,36; 4) -3.

Ответ:

А	Б	В

	Сократите дробь: .
1) ;	2) ;	3) ;	4) .

	Решите уравнение .
1) 0,25; 3;	2) 0,5; 6;	3) -0,25; -3;	4) -0,5; -6.

Прочитайте задачу: «Найдите стороны прямоугольника, если их разность равна 14 см, а диагональ прямоугольника – 26 см». Составьте уравнение, соответствующее условию задачи, если буквой х обозначена меньшая сторона прямоугольника (в см). Ответ: _______________.

	График какой из функций проходит через точку с координатами ?
1) ;	2) ;	3) ;	4) .

На рисунке изображен график функции . Укажите номера верных утверждений о данной функции. 1) Функция убывает на промежутке . 2) Функция определена для всех . 3) Функция принимает наибольшее значение при . 4) . Ответ: _______________.

Основание равнобедренного треугольника равно 16 см, а проведенная к основанию высота равна 15 см. Найдите периметр треугольника. Ответ: _______________.

Дата добавления: 2015-09-07