См капицу

19. Теоретическая интерпретация правила «ранг-размер» Дж. К. Зипфом. Возможности других интерпретаций.

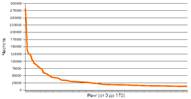
Правило «ранг-размер», в соответствии с которым, в списке городов страны или региона, составленном в порядке убывающей численности населения, людность города с порядковым номером n равна численности населения первого города, деленной на n, было впервые установлено в 1913г. Феликсом Ауэрбахом. Обычно используется следующая его запись: P_n = P₁ n^-1 В идеальном случае на графике с осями в логарифмическом масштабе, где по оси Х откладывается ранг города (его порядковый номер), а по оси Y – его людность, города ложатся на прямую, образующую угол в 45 градусов с осями координат. Статья Ауэрбаха была опубликована в солидном немецком географическом журнале “Peterman’s Mitteilungen”, однако географическое сообщество в начале ХХ в. еще не было подготовлено к восприятию формализованных теорий и последователей у Ауэрбаха, по всей видимости, не было.

В конце 30-х гг. правило «ранг-размер» было переоткрыто американским социологом немецкого происхождения Джорджем К.Зипфом (G.К.Zipf), который, предположительно, не знал о работах своего предшественника. В 1941г. вышла книга Зипфа «Национальное единство и разъединенность. Страна как биосоциальный организм (National Unity and Disunity. The Nation as a Bio-Social Organism. Bloomington, Ind, 1941)», из самого названия которой следует, что автор считал выявленную им закономерность проявлением некого закона, характеризующего территориальную организации городского расселения страны. По своим методологическим установкам Зипф стоял на эволюционистских позициях: в его книге, в частности приводится график распределения по размеру городов СССР по переписи 1926г., построенный, как и во всех прочих случаях, в логарифмическом масштабе, на котором Ленинград весьма заметно отклоняется вверх от теоретической прямой. Последнее обстоятельство легко объясняется тем, что этот город лишь за 8 лет до переписи утратил столичные функции, и еще не успел встать на место, положенное ему как второму городу страны.

Вторая книга Зипфа, вышедшая в 1949г. и имевшая несравненно больший резонанс, называлась «Человеческое поведение и принцип наименьшей затраты усилий (Human Behavior and the Principle of the Last Effort. Cambridge, Mass., 1949)». В ней автор изменил интерпретацию установленной им закономерности, что также следует из названия книги. Зипф рассматривал гипотетическую ситуацию, при которой все население страны сосредоточено в одном большом городе (“One Big City”). В таком случае использование территориии и ресурсов страны будет очень далеким от оптимального. Экономия усилий нации требует, по мнению Зипфа, наличия весьма значительного числа городов, людность которых подчиняется правилу «ранг-размер». Однако это правило не накладывает никаких ограничений на пространственное размещение городов, поэтому такие доводы едва ли могут быть убедительными.

Между тем во второй книге Зипфа показано, что отмеченная им закономерность выполняется далеко за пределами географии. Так, распределение газет по тиражу в крупных регионах США также подчиняется правилу «ранг-размер». Расцвет математической лингвистики в 60-е и 70-е гг. ХХ в. ознаменовался установление того факта, что распределение слов по частоте в любом целостном произведении также подчиняется правилу «ранг-размер», который у лингвистов принято называть законом Ципфа. Например, распределение слов по частоте в романе Л.Н.Толстого «Война и мир» и в его рассказе «Казаки» соответствует «закону Ципфа», но эта закономерность не будет выполняться для одного из томов «Войны и мира», или для какой-то части упомянутого рассказа.

Отмеченная закономерность позволяет рассматривать соответствие правилу «ранг-размер» как характеристику целостности системы, причем не только системы городского расселения. При этом эволюционный подход к изучению городского расселения побуждает искать объяснения отклонениям от правила «ранг-размер» именно в особенностях исторического развития, не позволивших сформироваться целостным системам городского расселения. Так, Варшава, со всей очевидностью, мала для такой страны, как Польша, что связано с драматической историей этой страны, собранной после Первой мировой войны из трех весьма разнородных частей и испытавшей сильнейшие территориальные изменения после Второй мировой войны. Понятно, что и наличие второй столицы (правильнее сказать – бывшей столицы), также обусловленное историческими причинами, существенно ухудшает соответствие предсказаниям правила «ранг-размер». Самые близкие примеры –Каунас в Литве и Харьков в Украине.

Закон Ципфа (Зипфа) — эмпирическая закономерность распределения частоты слов естественного языка: если все слова языка (или просто достаточно длинного текста) упорядочить по убыванию частоты их использования, то частота n-го слова в таком списке окажется приблизительно обратно пропорциональной его порядковому номеру n (так называемому рангу этого слова, см. шкала порядка). Например второе по используемости слово встречается примерно в два раза реже, чем первое, третье — в три раза реже, чем первое, и т. д.

Закон носит имя своего первооткрывателя — американского лингвиста Джорджа Ципфа (George Kingsley Zipf) из Гарвардского университета.

20. Чем вызвана необходимость использования коэффициента первенствования Ю.В. Медведкова?

В 1964г. Ю.В.Медведковым был предложен коэффициент первенствовования, использование которого позволяет как бы вынести за скобки гипертрофированные или, наоборот, «недоразвитые» столицы и после этого рассмотреть соответствие системы городского расселения правилу «ранг-размер». Сначала первый город исключается из рассмотрения, затем для остальных городов производится линейная аппроксимация теоретической прямой с помощью метода наименьших квадратов. При этом полученная прямая только в качестве редкого исключения будет образовывать угол в 45 градусов с осями координат, т.е. показатель степени при n будет либо больше, либо меньше единицы. Пересечение полученной прямой с осью Y дает теоретическую людность первого города, на которую и делится реальная людность первого города. Полученная величина и есть коэффициент первенствования, который может быть как больше, так и меньше единицы. Последнее имеет место в случае недостаточного развития национальных или региональных столиц.

Использование показателей степени при n, имеющих значение, отличное от единицы, позволяет в огромной степени улучшить соответствие между эмпирическими данными и предсказаниями теории и, соответственно, существенно расширить сферу применения правила «ранг-размер». Однако в таком случае соответствие эмпирического распределения теоретическому больше не может рассматриваться как характеристика целостности системы и теоретическое распределение превращается из характеристики фундаментальных свойств системы в простое средство аппроксимации (Аппроксимация (от лат. approximo — приближаюсь), замена одних математических объектов другими, в том или ином смысле близкими к исходным. А. позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). И в этом случае остается возможность измерять степень соответствия эмпирического распределения теоретически предсказанному, но теория не накладывает никаких ограничений на величину наклона прямой, которая в предельных случаях может быть сколь угодно близкой либо к горизонтальному, либо к вертикальному положению. Соответственно, в таком виде правило «ранг-размер» не позволяет формулировать фальсифицируемые, т.е. опровергаемые утверждения и, как следствие, не может рассматриваться в качестве научной теории.

21. Пригодно ли правило ранг-размер для описания любых систем городского расселения? Почему оно нашло применение далеко за пределами географии?

(ранг-размер) - модель расчета численности населения любого города страны (иерархия городов). Если территория представляет собой целостный экономический район, то население n-ого по размеру города составляет 1/n числа жителей самого крупного города.

для любых пригодно. но если использовать его как критерий целостности то только в что-то типа наших эк районов. с коэффициентами - можно для любых систем.

применяется не только с городами, так как является универсальным критерием целостности

Дата добавления: 2015-09-07