Иосилевич Г.Б. «Детали машин» 1988г. §14.7

В идеально точной цилиндрической передаче с эвольвентным зацеплением при отсутствии деформирующего усилия передаточное число –

u = 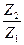= const в любой момент времени постоянно и в поле зацепления реализуются теоретические линии контакта. В реальных условиях, ввиду погрешностей изготовления и сборки эти условия не выполняются. Действительное значение передаточного числа u = отклоняются от постоянной величины. Это вызывает в зацеплении дополнительные динамические нагрузки, вибрации и шум. Реальная длина контактных линий составляет лишь часть их теоретической величины.

Наибольшее значение удельной нагрузки будет там, где зубья контактируют до приложения внешней нагрузки.

Нагрузка на зубчатые колеса рассчитывается исходя из:

а) полезной или номинальной нагрузки в предположении, что она распределена по длине зубьев равномерно;

б) дополнительной нагрузки на опасном участке длины зубьев, появляющейся вследствие упругих перекосов валов и начальных погрешностей изготовления – концентрации нагрузок;

в) дополнительной динамической нагрузки, связанной с погрешностями изготовления по шагу зубьев и другими факторами.

За расчетную нагружу принимают максимальное значение удельной погрузки, распределенной по линии контакта зубьев путем умножения номинальной нагрузки на коэффициент K.

q_n = ,

где F_n— нормальная сила в зацеплении;

l_Σ — суммарная длина линии контакта.зубьев.

K = Kα ·K β ·K_V — коэффициент расчетной нагрузки.

В расчетах соответственно используется символика:

при расчетах по контактным напряжениям – K нα ·K н_β ·K н_V;

при расчетах по напряжениям изгиба – K _Fα ·K _Fβ ·K _FV;

При приближенных (предварительных расчетах) коэффициент нагрузки можно принимать K = 1,3 … 1,5. Меньшие значения – при симметричном расположении зубчатых колес на валах, большие значения – при несимметричном и консольном.

Kα – коэффициент учитывает распределение нагрузки между зубьями при коэффициенте торцового перекрытия εα >1 (при двухпарном зацеплении)

K β — коэффициент концентрации нагрузки по длине зубьев;

K_v — коэффициент динамической нагрузки;

Коэффициент распределения нагрузки между зубьями – Kα

(при двухпарном зацеплении)

На рис. 7 изображено взаимное расположение зубчатых колес при двухпарном зацеплении,

где – А – пара зубьев первой вошедшая в зацепление;

В – пара зубьев вошедшая в зацепление после первой;

Kα = ,

где –

– коэффициент нагрузки в идеально точной передаче, в которой контакт пар зубьев в точках А и В наступает одновременно;

где q_n – удельная контактная нагрузка q_n = ;

Δ₀ – зазор между первой и второй парой зубьев;

λ_А – суммарная податливость пары зубьев первой вступившей в контакт;

λ_В – суммарная податливость пары зубьев второй вступившей в контакт.

Для косозубой передачи K нα =1…1,15; K _Fα =1 …1,4.

Для прямозубой передачи K нα = 1; K _Fα = 1.

Коэффициент учитывающий неравномерность распределения нагрузки

по длине контактных линий зубьев – K β

Коэффициент концентрации нагрузки К β. Концентрация или не­равномерность распределения нагрузки по длине зуба связана с де­формацией валов, корпусов, опор и самих зубчатых колес, а также с погрешностями изготовления передачи. Поясним это сложное явле­ние на примере, учитывающем только прогиб валов.

На рис. 8 изображено взаимное расположение зубчатых колес при деформированных валах в случаях: симметричного (рис. 8, а), несимметричного (рис. 8, б) и консольного (рис. 8, в) располо­жения колес относительно опор. Валы прогибаются в противополож­ные стороны под действием сил в зацеплении.

При симметричном расположении опор прогиб валов не вызывает перекоса зубчатых колес и, следовательно, почти не нарушает рас­пределения нагрузки по длине зуба. Это самый благоприятный случай. При несимметричном и консольном расположении опор колеса пере­кашиваются на угол у, что приводит к нарушению правильного касания зубьев. Если бы зубья были абсолютно жесткими, то они соприкаса­лись бы только своими концами (см. рис. 8, г, на котором изобра­жено сечение зубьев плоскостью зацепления). Деформация зубьев уменьшает влияние перекосов и в большинстве случаев сохраняет их соприкасание по всей длине

(рис. 8, д).Однако при этом нагрузка перераспределяется в соответствии с деформацией отдельных участков зубьев (рис. 8 е).

Рис.8

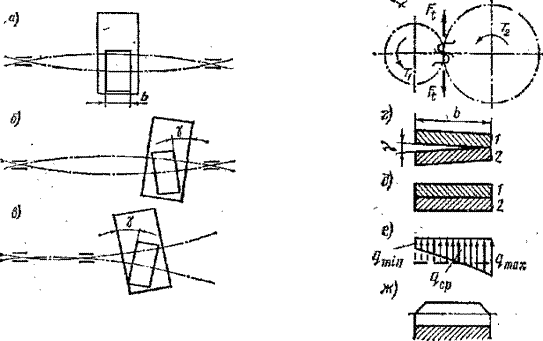
Отношение максимальной удельной нагрузки к средней по длине зуба называют

коэффициентом распределения нагрузки по ширине венца – K β.

K β= ,

где q_ср — средняя интенсивность нагрузки.

При прочих равных условиях влияние перекоса зубьев увеличивается с увеличением ширины колес b_w, поэтому ее ограничивают.

Концентрация нагрузки увеличивает контактные напряжения и напряжения изгиба. Для уменьшения опасности выламывания углов зубьев на практике применяют колеса со срезанными углами.

Если колеса изготовлены из прирабатывающихся ма­териалов (например, стали твердостью НВ<350 при Vt < 15 м/c), то концентрация нагрузки постепенно уменьшается вследствие повышенного местного износа. При постоянной нагрузке приработка зубьев может полностью устранить концентрацию напряжений.

Для прирабатывающихся колес различают начальный коэффициент – K _β⁰ и коэффициент после приработки, который приближенно можно принимать

K _β = 0,5·(K _β⁰+1)

Для уменьшения концентрации нагрузки следует повышать точность изготовления и жесткость валов и опор, выбирать благоприятное расположение валов относительно опор и т.п.

При НВ<350 и Vt < 15 м/c можно принимать K _β =1.

Коэффициент динамической нагрузки – K_v

Погрешность нарезания зубьев приводит к непостоянству мгновенных значений передаточного числа. В зацеплении появляется дополнительный динамический момент

Мv=J ,

где J – момент инерции ведомых масс.

Рис.9

Полная расчетная нагрузка на зубья с учетом динамики складывается из

Схема возникновения кромочного (а) и сре­динного (б) ударов зубьев

номинальной и приведенной динамической.

Основные динамические нагрузки в прямозубых колесах возникают при входе и выходе зубьев в зацеплении. Для безударной работы необходимо, чтобы

контакт зубьев происходил строго по линии зацепления при равенстве основных шагов под нагрузкой. На самом деле эти условия не выполняются и передача работает с ударом зубьев.

Кромочный удар зубьев возникает, если основной шаг ведомого колеса меньше ведущего. Происходит преждевременный вход в зацепление с зубом ведомого колеса (Рис.9,а).

Срединный удар зубьев возникает, если основной шаг ведомого колеса больше ведущего (Рис.9, б). Происходит преждевременный выход из зацепления предшествующей пары ведомого колеса. Ведущее колесо догоняет ведомое, выбирая зазор с ударом при входе в зацепление в срединной части зуба.

Динамическая нагрузка растет пропорционально скорости и массам и уменьшается при повышении точности изготовлении колес.

Коэффициент K_v определяется по формуле

K_v = 1 + ,

где q_v – удельная динамическая нагрузка;

q – удельная расчетная рабочая нагрузка.

При обычных технических расчетах K_v выбирается по таблицам в зависимости от степени точности, твердости материалов зубчатых колес и окружной скорости.

Дата добавления: 2015-09-05