Теоретические предпосылки

для расчета контактных напряжений.

Контактные напряжения образуются в месте соприкосновения двух тел в тех случаях, когда размеры площадки касания малы по срав­нению с размерами тел (сжатие двух шаров, шара и плоскости, двух цилиндров и т. п.). Если значение контактных напряжений больше допускаемого, то на поверхности деталей появляются вмятины, бо­розды, трещины или мелкие раковины. Подобные повреждения на­блюдаются у зубчатых, червячных, фрикционных и цепных передач, а также в подшипниках качения.

Теория контактных напряжений, являющаяся предметом курса «Тео­рия упругости», позволяет разработать инженерные методы расчета зубчатых передач и многих деталей машин. Основоположником теории контактных напряжений является H.Herz (1881).

При расчете контактных напряжений (Рис.5) различают два характерных случая: первоначальный контакт в точке (а – два шара, шар и плоскость и т. п.); первоначальный контакт по линии (б – два цилиндра с парал­лельными осями, цилиндр и плоскость, в – поверхности зубьев и т. п.).

На рис. 6 изображен пример сжатия двух цилиндров с параллель­ными осями. До приложения удельной нагрузки q цилиндры соприка­сались по линии. Под нагрузкой – Fn линейный контакт переходит в кон­такт по узкой площадке шириной 2b _Н. Силы взаимодействия между деталями пропорциональны деформациям и распределены по ширине указанной площадки неравномерно. В материале контактирующих деталей возникает объемное напряженное состояние – трехосное сжатие. При этом область максимального нормального напряжения σ _Нmax располагается на продольной оси симметрии контакт­ной площадки. Оно используется в качестве одного из критериев для суждения о работоспособности несовпадающих поверхностей. При этом величина σ _Нmax не должна превышать [ σ _Н], полученное экспериментом или опытом эксплуатации при аналогичных условиях работы в зоне контакта. Надежность контактирующих поверхностей определяется прочностью их рабочих поверхностей – контактной прочностью.

Если контактные напряжения постоянны или мало меняются во времени, то расчет ведут на статическую контактную прочность, нарушение которой приводит к появлению трещин (для хрупких материалов) или пластических деформаций.

При многократно циклически повторяющихся контактных напряжениях происходит усталостное разрушение (выкрашивание) рабочих поверхностей.

Принятые допущения при выводе расчетных зависимостей.

Величина σ _Нmax найдена в предположении идеально гладких поверхностей, однородности и изотропности материала, малого отношения площадки контакта к минимальному радиусу кривизны в зоне касания, отсутствия остаточных деформаций и нормального направления к поверхностям усилия между ними.

Значение этих напряжений вычисляют по формуле

σ_Нmax = 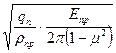, (1)

где q_n – удельная контактная нагрузка q_n = ;

ρ_пр – приведенный радиус кривизны, ρ_пр = ,

где – ρ₁ и ρ₂ радиусы кривизны цилиндров;

Е_пр – приведенный модуль упругости Е_пр = ,

где E₁ и E₂ — приведенные модуль упругости первого рода;

μ – коэффициент Пуассона

Для конструкционных металлов коэффициент Пуассона распола­гается в пределах μ = 0,25...0,35. Без существенной погрешности при­нимают μ =0,3

Формула (1) справедлива не только для круговых, но и для любых других цилиндров. Знак минус при расчете приведенного радиуса кривизны относится к случаю внутреннего контакта (когда поверхность одного из цилиндров вогнутая).

При начальном точечном контакте формула имеет вид:

σ_Нmax = m · ,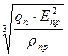

где ρ_пр – приведенный радиус кривизны в плоскости наиболее тесного контакта.

Для вязких материалов предельные контактные напряжения выбираются по условию полного отсутствия течения материала равными (2 – 3)σ_Т.

Предельные напряжения по критерию выносливости при перекатывании поверхностей выбираются в зависимости от твердости материалов

[ σ_Н ] = C_B· [HB], [ σ_Н ] = C_R· [HRC], где – C_B и C_R коэффициенты.

Дата добавления: 2015-09-05