Многозначные логики.

В многозначных логиках высказывания и предикаты могут принимать не 2 значения (истина или ложь), а более. Существует множество таких логик, находящих все большое применение. Рассмотрим здесь трехзначную логику Лукашевича и четырехзначную логику параллельных миров (логику возможных миров).

В логике Лукашевича возможно три истинностных значения: 0 – ложно, 1 – возможно, 2 – истинно.

Используются дополнительные кванторы (квантификаторы)?(29)

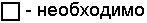
и?(30)

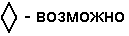
//таблицы истинности – рисунок (31)

F	ù F		Ù					Ú

F				↔
									F→G = ù FÚ G

Формула F ↔ G = (F → G) Ù (G Ù F) здесь не действительна.

Здесь, справедливы формулы:

//формулы (32)

ù (F Ú G) = ù F Ù ù G

ù (F Ù G) = ù F Ú ù G

В логике параллельных миров предполагается, что есть несколько миров текущий (X) и множество параллельных. Соответственно определено четыре истинностных значения.

A) Необходимо (абсолютно) истинно (3) – истинно как в текущем мире X, так и во всех параллельных мирах.

B) Случайно истинно (2) – истинно в текущем мире X, но может существовать мир Y, где высказывание (предикат) ложно.

C) Случайно ложно (1) – ложно в текущем мире X, но может существовать мир Y, где высказывание (предикат) ложно.

D) Необходимо (абсолютно) ложно (0) – ложно как в текущем мире X, так и во всех параллельных мирах.

Приведем таблицы истинности.

//таблицы истинности (33)

F	ù F		Ù

Ú						F
										F→ G = ù F Ú G

Особенностью этой логики является, что конъюнкция соответствует операции побитового «и», дизъюнкция – операции побитового «или», а отрицание – операции побитового отрицания (подробнее о побитовых операциях []).

Действительно, проведем вычисления.

//вычисления (34)

						and

not						not

Глава 3. ПРОДУКЦИОННЫЕ МОДЕЛИ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ

В данной главе рассматриваются продукционные модели представления знаний, которые являются ближайшей альтернативой логических моделей. Производится сравнение моделей этих типов.

Основные понятия

Продукцией или продукционным правилом называется правило вида:

ЕСЛИ условие ТО действие.

В рамках продукционной модели знания представляются в виде набора (системы) продукционных правил, которые задают возможности преобразования глобальной базы данных.

Пример. «Игра в восемь» (упрощенные пятнашки).

Задача. Дана доска, на которой девять клеток, по которым перемещается восемь фишек. Их следует расположить по порядку (см. рисунки? и?).

//рисунки – пример начального расположения фишек и правильное расположение фишек, которое должно получиться. (1)

Сформулируем правила. Условно считаем, что мы как бы перемещаем не фишки, а пустую клетку (дырку).

A) Если дырка не в верхнем ряду, переместить ее вверх.

B) Если дырка не а правом столбце, переместить ее вправо.

С) Если дырка не в левом столбце, переместить ее влево.

D) Если дырка не в нижнем ряду, переместить ее вниз.

//рисунок хода игры (2)

			←				↓				↓

			→				↑

Последнее состояние здесь является терминальным (правильная расстановка цифр).

Продукционные модели часто используются при построении ЭС. Эта модель удобна тем, что язык представления ГБД может выбираться произвольно в зависимости от задачи (в предикатных языках ГБД представляется в виде набора предикатов). Структура ЭС описана в 2.2.7. Здесь, вспомним, что конечная цель – достижение терминального состояния ГБД.

Пример. Формализация задачи о волке, козе и капусте. Есть река и лодка, в которую входит лодочник и еще один предмет. Козу и волка, а также козу и капусту нельзя оставлять вместе без присмотра. Задача – перевезти все с левого берега на правый.

Представление ГБД. (x,y,z,s).

x,y,z,s = 0 - соответствующий предмет на левом берегу

x,y,z,s =1 – соответствующий предмет на правом берегу

Таким образом, (0,0,0,0) – исходное состояние, а (1,1,1,1) – терминальное состояние.

Прежде чем сформулировать правила, необходимо отсеять недопустимые состояния. Таковыми являются состояния, предусматривающие одновременное нахождение волка и козы или козы и капусты на берегу, противоположном от лодочника. Допустимые правила должны обеспечивать отсутствие возможности перехода в недопустимые состояния.

Исходя, их этого соображения можно построить следующую таблицу:

Правило	Условие применимости
прямая перевозка волка – (0,y,z,0)->(1,y,z,1)	ù(y=0 Ùz=0)
прямая перевозка козы – (x,0,z,0)->(x,1,z,1)	всегда
прямая перевозка капусты – (x,y,0,0)->(x,y,1,1)	ù(x=0 Ù y=0)
прямая пустая перевозка	ù(y=0 Ù z=0) Ù ù(x=0 Ù y=0)
обратная перевозка волка – (1,y,z,1)->(0,y,z,0)	ù(y=1 Ùz=1)
обратная перевозка козы – (x,1,z,1)->(x,0,z,0)	всегда
обратная перевозка капусты – (x,y,1,1)->(x,y,0,0)	ù(x=1 Ù y=1)
обратная пустая перевозка – (x,y,z,1)->(x,y,z,0)	ù(y=1 Ù z=1) Ù ù(x=1 Ù y=1)

Очевидно, что на продукциях, можно поставить задачи четырех типов:

E) Определить существует ли решение вообще?

F) Найти любое решение задачи.

G) Найти всевозможные решения задачи.

D) Найти из множеств решений оптимальное в каком-либо смысле. При этом в простейшем случае, под оптимальным понимается решение, требующее как можно меньше операций преобразования ГБД. В более сложных случаях, приходится оперировать с весовыми коэффициентами, соответствующими правилам.

Дата добавления: 2015-09-06