Читайте также:
|
Векторной диаграммой называется совокупность векторов ЭДС, напряжения и токов, изображенных в одной системе координат. Наиболее распространенным типом векторной диаграммы является диаграмма, содержащая на комплексной плоскости комплексы действующих значений ЭДС, напряжения и тока.
Для построения векторной диаграммы напряжений определим комплексы напряжений на всех элементах цепи. Все значения полученные в показательной форме приведем к алгебраической.
=180В
= 
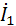· z 1=30e-j90⁰· 6ej90⁰=180(В)
= 
· z 2=22,5e-j60⁰· 8ej60⁰=180(В)
= 
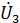· z 3=29,44ej28,73⁰· 5e-j90⁰=147.2e-j61.27⁰=147.2cos(-61.27⁰)+j147.2sin(-61.27⁰)=
=70.76 - j129.1(B)
= 
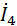· z 4=14,95ej4.76⁰· 11.31ej45⁰=169.12ej49.76⁰=169.12cos(49.76⁰)+
+j169.12sin(49.76⁰)=109.2 + j129.1(B)
= 
· z 5=16.912ej49.76⁰· 10=169.12ej49.76⁰=169.12cos(49.76⁰)+j169.12sin(49.76⁰)=
=109.2 + j129.1(B)
Для построения векторов нужно отложить угол ϕ и действующее значение синусоидально изменяющейся величины I и U. Амплитуду возьмем в масштабе.
Для тока =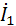 
30e-j90⁰= -j30(А)
ϕ=-90⁰, I=30
Аналогично определяются величины ϕ и I для векторов остальных токов.
Для напряжения =180
ϕ=0⁰, I=180
Аналогично определяются величины ϕ и I для векторов остальных напряжений.
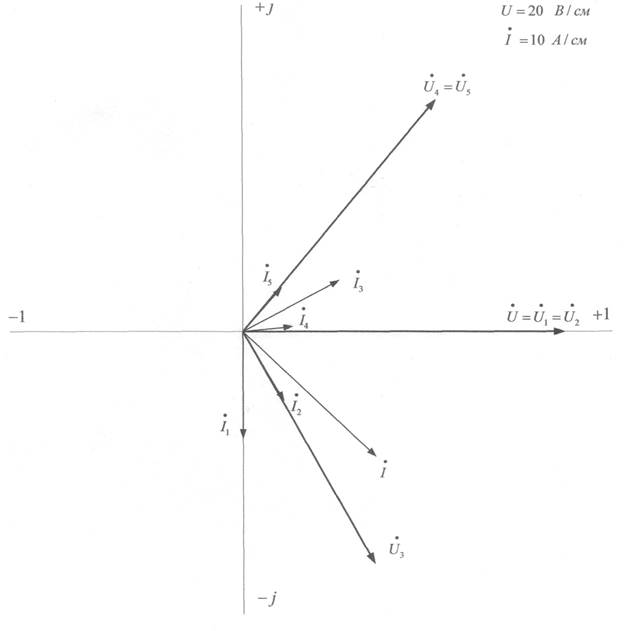
Векторная диаграмма напряжений и токов представлена на рисунке:
Дата добавления: 2015-09-06; просмотров: 541 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Указать на схеме условно положительные направления токов. Определить токи всех ветвей в комплексной форме. | | | Построить осцилограмму тока в ветви или напряжения на участке, определенном в задании. |