|
Читайте также: |
Изобразим схему замещения электрической цепи с обозначением характера сопротивлений всех ветвей.
Угловая частота колебаний в цепи:
ω=2πf=2·3,14·50=314(сек-1)
Согласно формуле Эйлера любая синусоидально изменяющаяся величина может быть представлена в комплексной форме
ejϕ=сosϕ+j·sinϕ
Переход от алгебраической формы a =b+jc к показательной a =ρejϕ выполняется по формулам:
a =b+jc= ρejϕ, где 
Обратный переход от показательной формы a =ρejϕ к алгебраической a =b+jc следует их формулы Эйлера:
a = ρejϕ= b+jc, где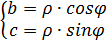 
Представим комплексы сопротивлений z 1 и z 2 в алгебраической форме:
z 1=6ej90⁰=6cos(90⁰)+j6sin(90⁰)=j6(Ом)
z 2=8ej60⁰=cos(60⁰)+j8sin(60⁰)=4+j6,93(Ом)
Представим алгебраическое выражение сопротивлений z 3 и z 4 в комплексной форме:
z 3=-j5=5e-j90⁰(Ом)
z 4=8+j8=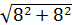 
ejarctg(8/8)=11,31ej45⁰ (Ом)
Схема замещения:
Указать на схеме условно положительные направления токов. Определить токи всех ветвей в комплексной форме.
Расставим условно положительные направления токов:
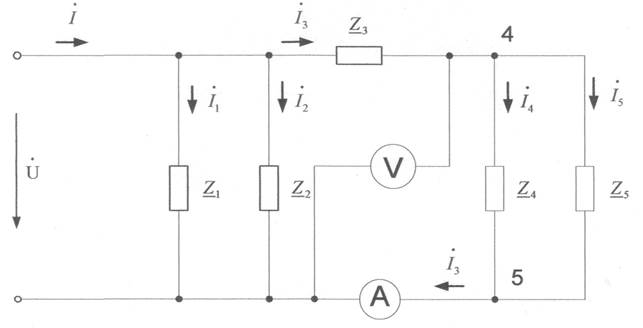
Для определения токов в ветвях в комплексной форме найдем эквивалентное сопротивление цепи.
Сопротивления z 4 и z 5 соединены параллельно, их эквивалентное сопротивление вычисляется по формуле: z 45=(z 4 · z 5)/(z 4 + z 5). В числитель подставляем показательные формы сопротивлений z 4 и z 5, а в знаменатель их алгебраические выражения, после алгебраических операций над знаменателем приводим его к показательной форме. Эквивалентное сопротивление получим в показательной форме и приведем его к алгебраической:
z 45= (z 4 · z 5)/(z 4 + z 5)=(11,31ej45⁰·10)/ (8+j8+10)=113,1ej45⁰/19,7ej23,96⁰=5,74ej21,04⁰=
=5,74cos(21,04⁰)+j5,74sin(21,04⁰)=5,36+j2,06(Ом)
После преобразования получим схему:
Сопротивления z 3 и z 45 соединены последовательно, их эквивалентное сопротивление вычисляется по формуле: z 345= z 3+ z 45. Найдем эквивалентное сопротивление в алгебраической форме и приведем его к комплексному виду: z 345= z 3+ z 45=-j5+5,36+j2,06=5,36-j2,94= 
ejarctg(-2,94/5,36)=
=6,117e-j28,73⁰(Ом)
После преобразования получим схему:
Сопротивления z 345 и z 2 соединены параллельно. Эквивалентное сопротивление получим в показательной форме и приведем его к алгебраической:
z 2345= (z 2· z 345)/(z 2+ z 345)=(8ej60⁰·6,117e-j28,73⁰)/(4+j6,93+5,36-j2,94)=
=48,91e32,27⁰/10,18ej23,09⁰=4,81ej8,19⁰=4,81cos(8,19⁰)+j4,81sin(8,19⁰)=
=4,76+j0,68(Ом)
После преобразования получим схему:
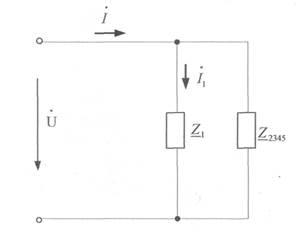
Сопротивления z 2345 и z 1 соединены параллельно. Эквивалентное сопротивление получим в показательной форме и приведем его к алгебраической:
z экв= (z 1· z 2345)/(z 1+ z 2345)=(6ej90⁰·4,818ej8,19⁰)/(j6+4,76+j0,68)=
=28,837e98,19⁰/8,32ej54,28⁰=3,5ej43,9⁰=3,5cos(43,9⁰)+j3,5sin(43,9⁰)=
=2,52+j2,43(Ом)
После преобразования получим схему:
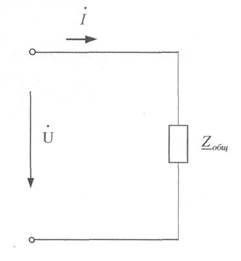
Найдем токи. Определим комплекс действующего значения тока в неразветвленной части цепи, используя закон Ома. Все значения, полученные в показательной форме приведем к алгебраической.
= 
= 
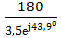= 51,39e-j43,9⁰=51,39cos(-43,9⁰)+j51,39sin(-43,9⁰)=
=37,03-j35,64(А)
= 
= 
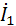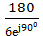= 30e-j90⁰=30cos(-90⁰)+j30sin(-90⁰)=-j30(А)
= 
= 
= 22,5e-j60⁰=22,5cos(-60⁰)+j22,5sin(-60⁰)=11,25-j19,49(А)
= 
= 
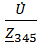= 29,44ej28,73⁰=29,44cos(28,73⁰)+j29,44sin(28,73⁰)=
=25,82+j14,15(А)
Найдем напряжение между узлами 4 и 5.
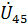= · z 45=29,44ej28,73⁰· 5,74ej21,04⁰=169,12ej49,76⁰=169,12cos(49,76⁰)+
+j169,12sin(49,76⁰)=109,2+j129,1(В)
= 
= 
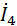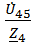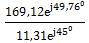= 14,95ej4.76⁰=14.95cos(4.76⁰)+j14.95sin(4.76⁰)=
=14.9+j1.24(А)
= 
= 
= 16,912ej49.76⁰=16.912cos(49.76⁰)+j16.95sin(49.76⁰)=
=10.92+j12.91(А)
Дата добавления: 2015-09-06; просмотров: 209 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПЕРЕПОСТ ЗООПСИХОЛОГА ОЛЬГИ КАЖАРОВОЙ | | | Построить векторную диаграмму токов и напряжений на комплексной плоскости. |