Потеряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации. Формула Ф.С.Ясинского.

При l меньше предельных (Для мягких строительных сталей l> 100, для сталей повышенной прочности l>85) стержни теряют устойчивость в упругопластической стадии работы материала с касательным модулем деформации Е_t= d s /de< Е.

Напряженно-деформированное

состояние центрально сжатого стержня: а — эпюра напряжений;

б — поперечное сечение стержня

Появляется дополнительный эксцентриситет а продольной силы. Приращение момента внешней силы dМ_е = N(n + а). Для внутренних сил d М_i определится суммой соответствующих интегралов по площадям А₁и А₂ разделенным нейтральной осью 2—2.

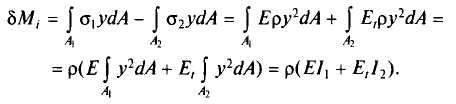
Тогда dМ_I = ρTJ, где Т представляет собой приведенный модуль деформации, определяемый из равенства TJ=EJ₁+E _T J₂. Откуда

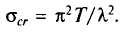
Введение понятия приведенного модуля Т эквивалентно замене стержня из разнородного материала (участок А₁ подчиняется упругому закону, участок А₂— пластическому) стержнем из однородного материала с уменьшенным модулем упругости.

Продолжая цепочку выкладок, напишем:

До сих пор рассматривался идеально прямой стержень с нагрузкой, приложенной строго по оси. В реальных конструкциях таких условий практически не существует. Ось стержня всегда имеет некоторые искривления, конструктивное оформление концов сжатых стержней не может обеспечить идеальную центровку сжимающей силы, что приводит к заметному снижению критических напряжений. Учет влияния указанных факторов осуществляется введением в расчет некоторого эквивалентного эксцентриситета сжимающей силы e_ef. Этот эксцентриситет зависит от многих случайных факторов: технологии изготовления, транспортировки, монтажа, конструктивного решения стержня и его узлов и т.д.

Статистические исследования эксцентриситетов показывают их зависимость от гибкости стержня — они возрастают с ростом гибкости. Поэтому в практических расчетах используют критическое напряжение, вычисленное с учетом случайных эксцентриситетов s_cr,е.

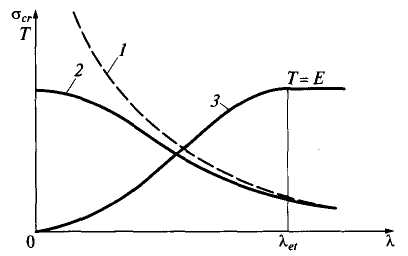Зависимость критических напряжений и приведенного модуля деформаций от гибкости стержня:

1 — кривая Эйлера; 2 — кривая критических напряжений для сталей типа СтЗ; 3 — график модуля Т

---

Дата добавления: 2015-09-06