Соединение зубчатых передач в ряды

ЛЕКЦИЯ 8

СЛОЖНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ

Соединение зубчатых передач в ряды

Передаточное отношение, которое можно осуществить одной парой зубчатых колес, невелико (i _max=15). На практике же часто приходится встречаться с необходимостью воспроизведения значительных передаточных отношений. Добиться этого можно путем использования нескольких зубчатых преобразователей, соединенных определенным образом в ряд. Сложные зубчатые механизмы подразделяются на рядные и на планетарные зубчатые механизмы.

В рядных механизмах звенья совершают простые движения – в основном вращательные и реже поступательные. В планетарных зубчатых механизмах отдельные звенья (зубчатые колеса) совершают сложные движения.

Рядные зубчатые механизмы (передачи) образуются путем последовательного или параллельного соединений трехзвенных зубчатых механизмов. Применительно к зубчатым механизмам наиболее часто используются следующие схемы соединения.

1. Последовательное соединение зубчатых передач. при такой схеме выходное колесо предыдущего преобразователя соединяется с входным колесом последующего. Общее передаточное отношение для зубчатых передач определится по зависимости

. (4.1)

При последовательном соединении ведомое звено звеном предыдущего механизма соединено с ведущем звеном последующего механизма (рис. 4.1), а сам механизм называется ступенью сложного механизма или передачи.

2. Комбинированное (последовательно – параллельное) соединение. Этот способ используется для создания нескольких параллельных потоков мощностей с целью улучшения условий нагруженных колес, валов и опор.

Структурная и кинематическая схемы одного из вариантов соединения приведены на рисунке 4.1, а, б.

а б

Рис. 4.1

в г

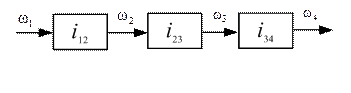
Рис. 4.2.

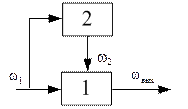
3. Комбинированное (встречно – параллельное) соединение (рисунок 4.1, в, г), встречается в дифференциальных замкнутых зубчатых механизмах. В таких механизмах параллельно основному зубчатому механизму 1 присоединяется от входа или выхода второй преобразователь 2, выходная величина которого подается снова в первый зубчатый механизм.

По конструктивному исполнению в зависимости от способа соединения колес схемы соединения а и выполняются в двух вариантах:

1. Каждое колесо имеет собственную неподвижную ось вращения (рис. 4.2, а).

2. В схеме имеются хотя бы два колеса, находящиеся на общей неподвижной оси вращения.

Оба варианта, имеющие неподвижные оси вращения колес, представляют так называемые рядные зубчатые соединения. Рассмотрим некоторые особенности этих соединений. В схеме по первому варианту угловые скорости вращения каждого колеса разные.

Формируя структурную схему, видим, что несколько колес одновременно входят в состав двух преобразователей. Учитывая, что передаточное отношение в зубчатой передаче i= ω_вх/ω_вых =Z _вых /Z _вх, для многорядного последовательного соединения на основании зависимости (4.1) запишем с учетом знака передаточного отношения

i _общ=(- i ₁₂)(- i ₂₃)(- i ₃₄)=(-ω₁ / ω₂)(-ω₂ / ω₃)(-ω₃ / ω₄)=

(4.2)

=(- Z ₂ / Z ₁)(- Z ₃ / Z ₂)(- Z ₄ / Z ₃)= - Z ₄ / Z ₁

Знак «минус» указывает, что в передаче происходит изменение направления вращения.

В общем случае при соединении n колес получим

i _общ=(-1) ^m Z_n / Z ₁. (4.3)

где m – число пар внешнего зацепления.

Из зависимости (4.3) видно, что величина общего передаточного отношения не зависит ни от размеров, ни от числа зубьев промежуточных зубчатых колес. Такая схема соединения не решает проблемы получения больших передаточных отношений. Она используется только для изменения направления вращения или же для увеличения межосевого расстояния между краснейшими колесами. Задача определения принципов соединений зубчатых пар в ряды для получения больших передаточных отношений может быть решена при рассмотрении второго конструктивного варианта соединения колес. В схеме из четырех зубчатых колес два имеют общую неподвижную ось вращения. При этом угловые скорости вращения этих колес равны между собой ω₂ = ω₃. Из анализа структурной схемы видно, что каждое колесо входит только в один преобразователь. Общее передаточное отношение всего механизма.

i _общ= ω₁ / ω₄= i ₁₂ i ₃₄=(-ω₁ / ω₂)(-ω₃ / ω₄)=

(4.4)

=(-Z₂ / Z₁) (-Z₄ / Z₃).

В общем случае имеем

i _общ =(- 1 )^{m .} (4.5)

При таким соединении каждое зубчатое колесо оказывает влияние на величину передаточного отношения.

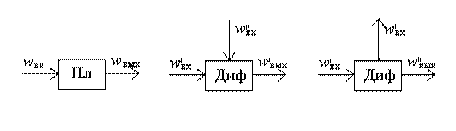
Кроме рассмотренных выше вариантов соединения зубчатых колес в ряды с неподвижными осями вращения, в технике находят широкое применение передачи, имеющие колеса с подвижными осями. Это так называемые эпициклические механизмы. В зависимости от степени подвижности эти преобразователи делятся на планетарные, имеющие входную и выходную величины (рисунок 4.3, а), и дифференциальные, у которых могут быть два выхода и входа (рисунок 4.3, б, в).

а б в

Рис. 4.3.

Эпициклический механизм состоит из двух центральных зубчатых колес (внешнего и внутреннего зацеплений), одного или двух колес с подвижной осью вращения, называемой водилом (рис. 4.4)

Центральные колеса и водило являются звеньями, связанными со входом и выходом. В зависимости от исполнения возможны следующие случаи преобразования величин:

а б

Рис. 4.4.

1. Одно из центральных колес (1 или 3) закрепляется неподвижно. Тогда вращение преобразовывается от другого центрального колеса на входе к водилу Н на выходе или в обратном направлении. Это будет планетарный механизм.

2. Оба центральных колеса могут вращаться, превращая эпициклический механизм в дифференциальный.

При этом может быть один вход от любого центрального колеса 1, 3 или водила Н и два выхода. Возможно существование обратного варианта: два входа (1, 3 или 4) и один выход.

Применяя встречно – параллельное соединение передач (рисунок 4.1, в, г), можно в дифференциальном механизме сделать взаимно – зависимыми две входные величины. Такой механизм называется замкнутым дифференциальным механизмом.

Планетарные зубчатые механизмы

Задача анализа теории работы механизмов с подвижными осями может быть решена на примере планетарных преобразователей.

Простейший трехзвенный планетарный механизм представлен на рис. 4.5. Он состоит из неподвижного колеса 3 с внутренними зубьями Z₃, подвижного центрального колеса 1 с зубьями Z₁, подвижного колеса – сателлита 2 с зубьями Z₂ и водила Н, на котором закреплена ось сателлита.

При вращении центрального колеса 1 начинает вращаться зацепленный с ним сателлит 2. Поскольку центральное колесо 3 неподвижно, то при вращении сателлита последний обкатывается вокруг колеса 3, заставляя вращаться водило Н.

Рисунок 4.5.

Наибольшее распространение в технике получили 4 – звенные планетарные механизмы (рисунок 4.4,б), полученные преобразованием двухступенчатой рядной передачи. Данный механизм имеет два центральных колеса (1 и 3) и водило Н и условное обозначение 2к – Н.

Для этого механизма число степеней подвижности W =1. и передача движения осуществляется от центрального колеса 1 к водилу Н или, наоборот, от водила Н к центральному колесу 1.

Для определения передаточного отношения эпициклического механизма воспользуемся методом обращения механизма (остановке водила). Условно сообщим всем подвижным звеньям дополнительное движение с угловой скоростью водила ω_Н в сторону, противоположную вращению последнего. Эпициклический механизм превращается в механизм с неподвижными осями, передаточное отношение которого рассмотрено выше. Угловые скорости вращения звеньев в обращенном механизме будут: водила ω _Н - ω _Н = 0, колеса 1 ω ₁= ω ₁ - ω _Н, колеса 3.

ω₃= ω₃ - ω _Н. Передаточное отношение обращенного механизма от первого колеса к третьему при неподвижном водиле определиться

. (4.6)

В общем случае для любого эпициклического механизма получим

, (4.7)

где - передаточное отношение обращенного механизма с неподвижными осями.

Для планетарного механизма, приведенного на рис. 4.7, при условии закрепления колеса 3 получим

, (4.8)

где - передаточное отношение планетарной зубчатой передачи.

Отсюда с учетом зависимости (4.6)

. (4.9)

При ведущем водиле получим

. (4.10)

Кроме рассмотренной схемы трехзвенного механизма существуют планетарные передачи с четырьмя подвижными звеньями. Конструктивно они выполняются в трех вариантах (рисунок 4.6, а, б, в) и состоят из двух центральных колес 1 и 4, водила Н и двух сателлитов 2 и 3, установленных на общей неподвижной оси.

а б в

Рис. 4.6.

В таком механизме имеются две пары зацепляемых колес 1-2, 3-4 внешнего зацепления (рисунок 4.6, а), внутреннего зацепления (рис. 4.6, в) или одна – внешнего и одна – внутреннего зацеплений (рисунок 4.6, б).

В 4 – звеном планетарном механизме передаточное отношение обращенного механизма определиться на основании зависимости (4.5):

а) для схемы на рисунке 4.5, а, в

; (4.11)

б) для схемы на рисунке 4.5, б

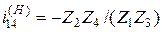. (4.12)

Тогда передаточное отношение планетарного механизма с закрепленным колесом 4 на основании формулы (4.7) будет для схемы на рисунке 4.6, а, в.

; (4.13)

и для схемы на рисунке 4.6, б

. (4.14)

Планетарные механизмы при ведущем водиле позволяют получить большие величины передаточного отношения.

Для механизмов по схеме на рисунке 4.6, а, в необходимо, чтобы передаточное отношение обращенного механизма было близко к единице. Тогда

(4.15)

будет стремиться к бесконечности, но при этом КПД сильно уменьшается. Например, при =1000КПД равен 0,1.

Проблема получения высокого значения КПД ограничивает величину передаточного отношения планетарного механизма. Для каждой схемы зубчатого механизма существует диапазон передаточных отношений, при котором механизм обладает оптимальными свойствами (минимальными массой и габаритами, наибольшим КПД, возможностью конструктивного исполнения, технологичностью и др.)

Дата добавления: 2015-09-05