
Читайте также:
|
Для анализа структурной надежности сети связи необходимо использовать следующие основные формулы надежности:
А) надежность системы rst, представляемой последовательностью ребер (i,j) (рис. 6) с вероятность pst безотказной работы ребра (i,j) определяется произведением вероятностей:
rst= 


a) б)


г) в)

д)
Рис. 6
б) надежность системы rst, представленной параллельными соединениями ребер k (рис. 6 б) определяется по формуле:
rst=1- 
в) основой расчета надежности сетей более ложной конфигурации является идея последовательного упрощения структуры. Сеть с мостиковым соединением приведена на рис. 6 в.
Надежность системы представляется формулой:
rst=pс*pst(pc=1)+(1-pc) pst(pc=0)
Система (st) при pc=1 преобразуется в сет с совмещенными вершинами 1 и 2 (рис. 6 г), а при pc=0 – в сет с параллельно – последовательным соединением (рис. 5 д).
В первом случае
pst(pc=1)=[  [
[ 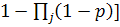
pst=[1-(1-pa)(1-pd)][1-(1-pb)(1-pm)]=(pa+ pd - pa* pd)(pb+pm – pb*pm)
Во втором случае:
pst(pc=0)=1-(1-pa*pb)(1-pd*pm)= pa* pb+ pd*pm- pa* pb* pd*pm
Надежность мостиковой структуры равна:
pst=pc(pa+pd – pa*pd)(pb+pm – pb*pm)+(1-pc)(pa*pb+pd*pm - pa*pb* pd*pm)
Подсчитаем вероятность безотказной работы анализируемой выше сети. Структура ее – мостиковая, следовательно, упрощение выполняется так, как описано выше.
p26=pn[(pm+pe-pm*pe)(pb*pd+pc-pb*pd*pc)]+(1-pn)(pe*pd*pb+pm*pc- pe*pd*pb *pm*pc)=0,8*0,96*0,928+0,165=0,877
p16=0,8*0,877=0,702
Надежность разговорного тракта без дополнительных связей (2-3) и (4-5) равна:
r(μ12346)=0,83=0,512
Построения плана распределения каналов вторичной сети
Задача создания вторичных некоммутируемых сетей актуальна как для сетей передачи индивидуальных сообщений, так и для сетей передачи массовых сообщений. При синтезе некоммутируемых вторичных сетей необходимо на базе каналов заданной емкости первичной сети образовать путем кроссирования в узлах пучки прямых каналов необходимой емкости.
Сформулированная задача называется задачей построения плана распределения каналов вторичной некоммутируемой сети. Для ее формализации и решения введем некоторые обозначения.
Структуру первичной сети будем изображать в виде графа, ребрам которого приписываются некоторые значения – веса (стоимости, длины) и пропускные способности в числе каналов.
Рассмотрим сеть, состоящую из 6 вершин и 8 ребер (рис. 6). Необходимо построить план распределения каналов при котором емкость пучка между вершинами 1 и 4 равнялась 24, между вершинами 2 и 5 – 20, между вершинами 3 и 6 – 16 каналам, т.е. Y14=24, Y25=20, Y36=16; при этом число транзитных участков в каждом пути не должно превышать трех.
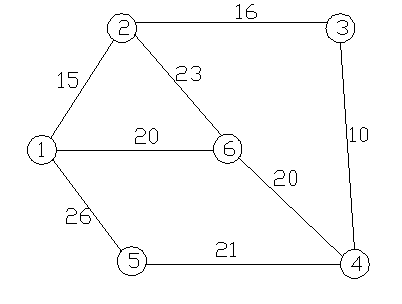
Рис. 7 – Структура первичной сети, изображенная в вид графа
Путь между вершинами i и j будем представлять упорядоченным набором узлов (или набором ребер).
Например, вершины 1 и 3 могут быть соединены путями:
μ351={3,4,5}; μ352={3,2,1,5}; μ353={3,2,6,4,5}; μ354={3,2,6,1,5}; μ355={3,4,6,2,1,5}; μ356={3,4,6,1,5}.
Рангом пути называется количество входящих в него ребер. В соответствии с определением:
r(μ131)=2, r(μ132)=3, r(μ133)=4, r(μ134)=4, r(μ135)=5, r(μ136)=4.
По соображениям качества связи ранг пути часто ограничивается, в частности для рассматриваемой задачи необходимо при построении пучка прямых каналов использовать только пути, ранг которых не превышает 3, т.е. пути μ131 и μ132.
Для решения задачи применим приближенный метод, который представим последовательностью повторяющихся шагов.
Шаг 1. Для каждой пары вершин (i, j), для которой необходимо построить пучок прямых каналов, строится множество путей и выбираются те из них, чей ранг удовлетворяет ограничению.
Шаг 2. Требуемое количество каналов Yij делится поровну между путями.
Шаг 3. Строится матрица емкостей допустимых путей, представляющая собой таблицу, строки которой соответствуют путям μi,j…k и столбца (i, j) записывается число каналов х этого ребра, выделенных для данного пути, т.е.
хijμ i,j…k
Сумма элементов каждого столбца показывает количество каналов этого ребра. Этот план распределения каналов построен без учета ограничения на количество каналов и называется идеальным.
Шаг 4. Проверяются выполнение ограничений на каждом ребре. Если они выполняются, задача решена, переход к шагу 6 – конец решения. В противном случае – к шагу 5.
Шаг 5. Для перенасыщенных ребер производится разгрузка (если возможно) и переход к шагу 4. Если разгрузить некоторые ребра невозможно – переход к шагу 7.
Шаг 6. Выдается план распределения каналов и останов.
Шаг 7. Решение невозможно из-за недостаточной емкости сети.
Для данного примера варианта:
Шаг 1. Построим множество путей рангом  3.
3.
μ131={1,5,4}; μ132={1,6,4}; μ133={1,2,6,4}; μ134={1,2,3,4};
μ251={2,1,5}; μ252={2,6,4,5}; μ253={2,6,1,5}; μ253={2,3,4,5};
μ361={3,4,6}; μ362={3,2,6}; μ363={3,2,1,6};
Шаг 2. Количество каналов делится поровну на все пути
х154=х164=х1264=х1234=24/4=6;
х215=х2645=х2615=х2345=20/4=5;
х346=х326=х3216=16/3=5,3 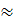 5
5
Таблица 2
| Yij | Емкость пути | Ребра | ||||||||
| 1-2 | 1-5 | 1-6 | 2-6 | 2-3 | 3-4 | 4-5 | 4-6 | |||
| Y14 | х154 | |||||||||
| х164 | ||||||||||
| х1264 | ||||||||||
| х1234 | ||||||||||
| Y25 | х215 | |||||||||
| х2645 | ||||||||||
| х2615 | ||||||||||
| х2345 | ||||||||||
| Y36 | х346 | |||||||||
| х326 | ||||||||||
| х3216 | ||||||||||
| Dхij1 | -2 | -1 | -1 | -1 | ПРК недоп. | |||||
| Dхij2 | Допуст. |
Шаг 3. Построим матрицу емкостей (Таблица 2).
Столбцы матрицы соответствуют ребрам заданной сети: (1-2), (1-5),…,а строки путям μijk.
Шаг 4. Просуммируем количество каналов в каждом столбце и, учитывая, что емкость каждого ребра равна 20, проверим условие

где М – множество всех допустимых путей, проходящих через ребро (i-j).
Подсчитаем
Dх=20- 
и запишем в |М|+1 строку. Отрицательная величина Dх говорит о недопустимости анализируемого плана распределения каналов и необходимости его корректировке
При перегрузке канала снимаем лишнюю нагрузку с ребра, входящего в данный путь, и следовательно, со всех ребер этого пути. Добавим эти каналы к недогруженным ребрам пути этого же пучка.
В итоге проверка показывает, что перегруженных ребер нет, следовательно план допустим.
Решение окончено: построен план распределения каналов, удовлетворяющий заданным условиям.
Заключение
В процессе курсовой работы были изучены различные принципы построения систем и сетей электросвязи, основы управления сетью, построение единой автоматизированной сети связи, рассмотрены математические методы анализа и расчета показателей сети.
Курсовой проект включал в себя изучение теоретического материала, выполнение практических работ.
Создание ЕАСС – исключительно сложная задача, решение которой рассчитано на много лет, требует значительных материальных затрат и участия большого числа специалистов.
Дата добавления: 2015-10-13; просмотров: 143 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Анализ фрагмента сети | | | Законопроектом предлагается исключить из ФЗ № 442 подпункт 1 пункта первого статьи 29. |