Спрямована кристалізація.

Розглянемо очищення при спрямованій кристалізації. Якщо речовину розплавити розплавити, а потім поступово охолоджувати, то при визначеній температурі з розплаву почнуть рости кристали. У загальному випадку концентрація домішкових атомів F в двох фазах неоднакова.

Як зазначено вище, у багатьох випадках можна записати:

(1.3)

де індекс l означає рідку, а s тверду фазу. Коефіцієнт коефіцієнт розпреділення k залежить тільки від температури. Величина k може бути більше або менше 1 і пов'язана з видом фазової діаграми таким чином, що значення k <1 відповідає тому випадку, коли домішкові атоми знижують точку плавлення речовини (рис. 1.1 (I); 1.2, а), а при k > 1 їх присутність підвищує точку плавлення (рис. 1.1 (II); 1.2,6). В обох випадках коефіцієнт розподілу k дорівнює р/q (рис. 1.2).

Якщо k <1, то при кристалізації розплав збагачується домішками F. Простежимо за схемою рис. 1.2,а за процесом кристалізації при русі фігуративного точки по шляху 1-2 (початок кристалізації) -3. Якщо розплав знаходиться в посудині довгастої форми, наприклад в циліндрі, і кристалізація починається з одного кінця цієї судини, то кристали, що виділилися спочатку, виявляються найбільш чистими. Їхня будова відповідає координаті 2'. Кристали, що утворюються пізніше, в процесі кристалізації поступово збагачуються домішкою F, а координата твердої фази по діаграмі 1.2, а переміщується від координати 2' до 3'.

Якщо k>1, то спостерігається зворотна картина; в цьому випадку у міру кристалізації розплаву він стає все чистіший, і фігуративна точка розплаву переміщається по шляху 1-2-3 на (рис. 1.2,б). Отже, виокремленні з нього кристали також очищаються від домішки F. При цьому фігуративна точка твердої фази опускається від точки 2' до 3' на рис. (1.2, б).

Рис. 1.1 Діаграми плавлення бінарних систем. Введення другого компонента призводить до зменшення (I) чи збільшенню (II) координати плавлення.

Рис.1.2. Склад кристалів (S), що знаходяться в рівновазі з речовиною (L); k=c_s/c_l=p/q. а-домішок який зменшує координату плавлення (k>1). Шляхи кристалізації: 1-2, 2’-3, 3’.

В рівноважних умовах концентрація домішок в кристалі визначається співвідношенням:

c_s=kc₀(1-g)^k-1

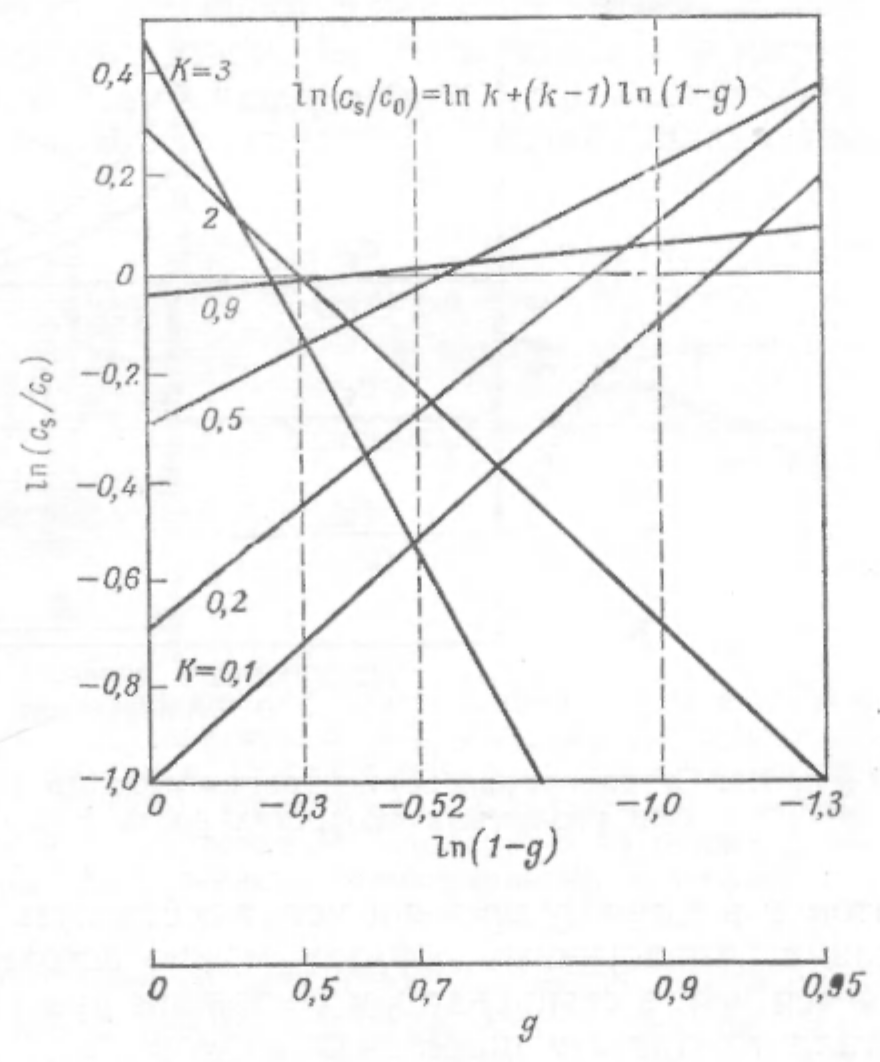
ln(c_s/c₀)=lnk+(k-1)ln(I-g), (1.4)

де c₀ - вихідна концентрація розчиненої домішки в розплаві, а g -частка закристалізованого розплаву. Вираз (1.4) або відповідний графік залежності ln(c_s/c₀) від In(1-g) або lg(c_s/c₀) від lg(1-g) дозволяють найбільш просто розрахувати k за експериментальними даними (рис. 1.3). Деякі значення k наведено в (табл. 1.2).

Ускладнення виникають через те, що коефіцієнт розподілу k не є величиною постійної. По-перше, з теорії випливає, що постійним являються співвідношення між активностями, а не між концентраціями і при цьому коефіцієнти активності, як правило, змінюються з концентрацією. По-друге, значення k залежить від температури, k =f/(Т). Але, оскільки домішок впливає на температуру тверднення (рис. 1.1), чисельне значення k залежить також і від концентрації домішки [2]. Правда, при низьких концентраціях домішок вказані малі ефекти і їх можна не враховувати.

РРис. 1.3. залежність c_s /c₀ від долі закристалізованого розплаву при направленній кристалізації (Пфані [1])

Більш серйозне ускладнення пов'язано з тим, що в реальних умовах росту кристалів система не знаходиться в рівновазі. Для обліку ефектів, пов'язаних з відхиленням системи від рівноважного стану, висвітленні різні теорії. Бартон, Прим та Сліхтер [3] показали, що основна відмінність між ідеальною рівновагою і перебуваючи, реалізованим в умовах росту кристалів, пов'язане з процесами, що відбуваються в розплав. Вміст домішок в кристалі і розплаві неоднаковий, тому концентрація речовини в напрямку від зростаючого кристала змінюється. Концентрація домішки F в розплаві не посередньо перед фронтом кристалізації більша, ніж в решті частини розплаву, якщо k <1, і менше, якщо k>1. У незмішуваному розплаві встановлюється градієнт концентрації, який викликає дифузію домішки F. Це зменшує, але ніколи не знищує повністю різниці концентрації. В результаті встановлюється стаціонарний стан при якому коефіцієнт розподілу k змінюється – він приймеє деяке значення k_efl при чому концентрація речовини в розплаві по близу зростаючого кристалу може значно відрізнятися від концентрації в об'ємі розплаву. Якщо розплав перемішується механічно або в результаті теплової конвекції, а на практиці так завжди і відбувається, то концентраційні відмінності в обсязі рідини усуваються. Однак в рідкому шарі поблизу поверхні розділу рідкої і твердої фаз потік виявляється ламінарним і перемішування утруднено. Тому дифузія в цьому шарі завжди залишається визначальним чинником і призводить до концентраційних розподілів, відповідним значенням k_efl лежачим в межах k< k_efl<1 (рис. 1.4). У загальному випадку товщина шару б, в якому дифузія відіграє вирішальну роль, залежить від швидкості перемішування. Якщо D - коефіцієнт дифузії домішки F в розплаві і V -швидкість росту кристала, то ефективний коефіцієнт розподілу описується виразом:

(1.5а).

Ця формула показує що k змінюється неправильно,від k_efl= k при малих швидкостях росту кристалів до k_efl=1 при більших швидкостях росту. Наприклад D=10^-5-10^-4см²/с. і =10^-2-10^-3см. Можна очікувати що k_eft~1 при v≥10^-2см/сек. Однак у тих випадках, коли розплав не перемішується і, отже, б збільшується, таке ж значення k спостерігатиметься при менших швидкостях росту.

Інша теорія запропонована Термондом [4]. У ній детально розглядаються процеси переносу атомів між зростаючим кристалом і розплавом. Якщо с_s і c_l - концентрації домішкових атомів в кристалі і розплаві, v_sl і v_ls швидкості їх перенесення з твердої фази в рідку і навпаки, то при рівновазі v_sl с_s - v_ls с_l або k = с_s/с_l = v_ls / v_sl. Швидкість перенесення v_sl можна записати у вигляді v_sl = а / 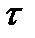, де а - глибина, з якою досить велике число атомів в одиницю часу можуть досягнути поверхні, а - час релаксації.

Рис. 1.4. стаціонарна концентрація суміші по біля вирощуваного кристалу для k<1 при різних швидкостях росту v (Бартон, Прім, Сліхтер[3]).

Аналогічним способом можна тлумачити і величину v_ls. Вважатимемо, що в стаціонарному стані при швидкості росту кристалу v в кристал входить с_sv домішкових атомів

с_sv-с_lv_ls-с_sv_sl

де с_lv_ls - кількість атомів, що перейшли з розплаву в кристал і с_sv_sl- кількість атомів що перейшли з кристалу в розплав. Використовуючи цей вираз отримаємо наступне рівняння:

однак воно не враховує того, що при кристалізації концентрація домішкових атомів захоплених кристалом співпадає з концентрацією їх в розплаві лиш в тому випадку коли перехід атомів між фазами відсутній. А різниця між с_sv_l і с_lv яка рівна числу атомів, що перейшли з однієї фази в іншу

.

Звідси можна отримати шуканий вираз для ефективного коефіцієнту розподілу.

(1.5б)

Згідно з цим виразом, k_efl =v_ls*v_sl - k при v – 0 і k_efl - 1 при v=∞.

В теорії, запропоновані Холлом [6], залежність k_efl від швидкості росту пояснюється утворенням абсорбційного шару на межі поділу фаз.

Згідно теорії Холла, домішкові атоми спочатку адсорбуються на поверхні розділу і лише потім входять в ришітку кристала. Таким чином, при великих швидкостях росту розподіл домішка між фазами відповідає адсорбційній рівновазі, а не рівновазі між об’ємом кристалу і розплаву. Якщо k_ads < k, то вміст домішка в кристалі виявиться більш високим, ніж це відповідало б рівновазі між об’ємом кристала і розплавом. Для k_efl Холл отримав вираз:

(1.5в).

де v- швидкість росту, v_sl – швидкість переносу домішкових атомів між кристалом і прилеглим до нього розплаву. Відповідно виразу (1.5в) k_efl=k, коли v_sl=v, і k_efl=k_ads, при v=v_sl. Залежність k_efl від v схематично показано на рис. [ (1.5,в) крива 1]. Теорія холка була

Рис. 1.5, а – концентраційна діаграма в кристалі з абсорбційним шаром атомів для рівноваги кристал – легований розплав при v=0, k_ads>I, k<I; б – розподіл домішок в зростаючому кристалі і розплаві при різних швидкостях росту v₁<v₂<∞; в – схематичні криві залежності ефективного коефіцієнта розплаву від швидкості росту: 1-за теорією Р. Холла; 2-за теорією Бартона-Пріма-Сліхтера для k_ads; 3-згідно комбінованої теорії.

підтверджена подальшими дослідженнями залежності коефіцієнта розподілу від типу граней кристала, причому відмінності між коефіцієнтами розподілу для різних граней виявилися більшими, ніж було установлено в дослідах Холла. Більш того, було виявлено, що в залежності від швидкості росту k_eft (може змінюватися від k_eft <1 до k_eft > 1. Так, Беннетт і Лонжин [7] показали, що в умовах дуже швидкого зростання (зростання дендритних стрічок) для індію та алюмінію в германію величина k_eft складає відповідно 5 і 2, в той час як квазірівноважна величина при низьких швидкостях росту становить тільки 10^-3 і 10^-1. Така зміну не можна пояснити з точки зору уявлень Бартона-Прима-Сліхтера або Термонда. В загальному випадку необхідно враховувати і дифузійні процеси в рідині, тобто розширити теорію Холла, об'єднавши її з теорією Бартона та ін.

На (рис. 1.5, а) для статичних умов (v = 0) зображено розподіл домішки між кристалом з адсорбційним шаром і розплавом. При низьких швидкостях росту (v_sl >> v) адсорбційний шар рухається перед поверхнею розділу і підтримується за рахунок швидкого виходу на поверхню твердої фази тих атомів, які спочатку були адсорбовані і захоплені зростаючим кристалом. Якщо в розплаві домішка розподілена нерівномірно, що лежить в основі теорії Бартона-Прима-Сліхтера, то розподіл домішки повинно відповідати значенням k <1 (рис. 1.5, б; v = v₁). При більш високих швидкостях росту, коли, відповідно до теорії Холла, величина v стає рівною v_sl або перевищує це значення, адсорбційний шар все більшою мірою захоплюється кристалом. Отже, для підтримання складу адсорбційного шару домішкові атоми повинні дифундувати від розплаву до кристалу тим швидше, чим більше швидкість росту v. Тому в розплаві виникає градієнт концентрації домішки в напрямку, протилежному тому, яке було раніше, і, таким чином, перед кристалом утворюється збіднена область (рис. 1.5, б; v-v₂). При подальшому збільшенні швидкості росту збіднення область зростає і, врешті-решт, концентрація в рідкій і твердій фазах вирівнюється: с_s = c_l або k_eft = 1 (рис. 1.5, б; v>∞). Вираз для k_eft можна отримати, якщо замість k до в рівняннi (1.5a) підставити з рівняння (1.5в)

(1.5г)

Цей вираз збігається з тим, яке виведено з адсорбційної теорії, якщо D>> v Воно дає звичайне рівняння Бартона-Прима-Сліхтера (1.5a) при k_ads = k до відповідного рівняння, в якому k замінено на k_ads, якщо v_sl >> v.

У відповідності з виразом (1.5г) величина k_eff змінюється від k_eff = k при низьких швидкостях росту до k_eff =I при великих швидкостях росту. За умови що k_ads >I>k, величина k_eff. проходить через максимум, а при k_ads < k може проходити через мінімум. Однак при k<k_ads<1 величина k_eff змінюється монотонно. При k> I умовою максимуму є нерівність k_ads > k, а умова мінімуму - k_ads<1. Екстремум відсутній при k > k_ads > 1. На рис. (1.5в) крива 3 схематично показує залежність величини k_eff від швидкості росту v, крива 2-ті зміни, величини k_ads яких слід очікувати на основі теорії Холла, а крива 1 відповідає теорії Бартона-Прима-Сліхтера. Кожній кристалографічної грані відповідає певна величина k_ads, цю теорію можна перевірити, вивчаючи залежність k_eff від швидкості росту v для граней різного типу. В досить широкій області значень v такі виміри поки не проведені.

Розглянуті вирази отримані при допущенні, що кристал росте безперервно. Цілком можливий (принаймні для деяких граней) і ступінчасте зростання, здійснюваний послідовним додаванням шарів певної товщини. Виходячи з цього, А. А. Чернов провів теоретичний аналіз моделі Холла, припускаючи, що кристал росте шляхом приєднання з постійною частотою шарів певної товщини. Загальний результат дуже подібний з висновками Холла, причому значення k_eff змінюються монотонно від k_eff = k при низьких швидкостях росту до величини, очевидно збігається при великих швидкостях росту. Тому виявляється вірогідним, що при такому підході істотно не зміняться також і результати, до яких призведе використання й інших розглянутих вище моделей.

Ще одна теорія коефіцієнта розподілу, заснована на уявленні про шаровому зростанні, запропонована Трейнором з співробітниками. Передбачається, що кожен новий шар, далі росте дуже швидко (зі швидкістю v₈). У цих умовах швидкість утворення зародків визначає швидкість виникнення нових шарів, а отже, і фактичну швидкість росту (v) кристалу. А.А. Чернов, так само як Холл і Термонд, враховував швидкість процесів переносу між кристалом і розплавом в напрямку, перпендикулярному до поверхні розчину (кристал-розплав). Трейнор і співробітники розглядають ефекти Бартона-Прима-Сліхтера в рідині зростаючого шару, тобто в напрямку, паралельному основної поверхні розділу, що призводить до виразу

(1.5д)

в якому D-коефіцієнт дифузії домішкових атомів, а і 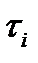-середні часи життя атомів розчинника і розчиненої речовини в адсорбційному шарі; 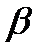-коефіцієнт, що залежить від і параметра, що описує перенос атомів з адсорбційного шару в розплав. Відповідно до виразу (І.5д) змінюється від k при малих величинах v_s до при великих значеннях де v_s, де .

Слід зазначити, що в цій моделі k_eff визначається величиною v_s а не v. Залежність k_eff від v можна отримати, якщо розглянути спільно теорію Трейнора і теорію Бартона-Прима-Сліхтера. Для цього у виразі (1.5a) замість k необхідно підставити k_eff з рівняння (1.5д).

Дата добавления: 2015-10-13